ME 417 - Numerical Lesson #1

Back to Lessons

PART I: SIMULATING A SYSTEM RESPONSE

In this part you will be simulating a general second-order dynamic system using different numerical methods, and you will also be exploring the effect of changing the system parameters on the response.

The general form of a second-order dynamic system represented by Figure 1, is given by the transfer function

Where $\omega_{n}$ and $\zeta$ are given by the definitions: $\omega_{n} = \sqrt{\frac{K}{M}}$, $2\zeta\omega_{n} = \frac{f_{v}}{M}$

EXERCISE 1

Given the following parameters: $M = 7\text{kg}$, $K = 2.8N\text{/}m$, $f_{v} = 1.5N - s\text{/}m$

Simulate the response of the system to a step input using the command step() in MATLAB. Repeat the step simulation with $f_{v} = 5$, and $f_{v} = 20$. Plot the three responses on the same plot. Explain the observed difference between the three responses.

Using the command step() is useful for analyzing a system's response to a simple and constant input to a system, but what if the input varies? We can instead use the command lsim().

clear all;
M = 7;
K = 2.8;
fv = [1.5 5 20] ;
wn = sqrt(K/M);
figure()
hold on
for ix = 1:3
zeta = fv(ix) / (M * 2 * wn);    
sys = tf([wn^2], [1 2*zeta*wn wn^2]);
step(sys)
end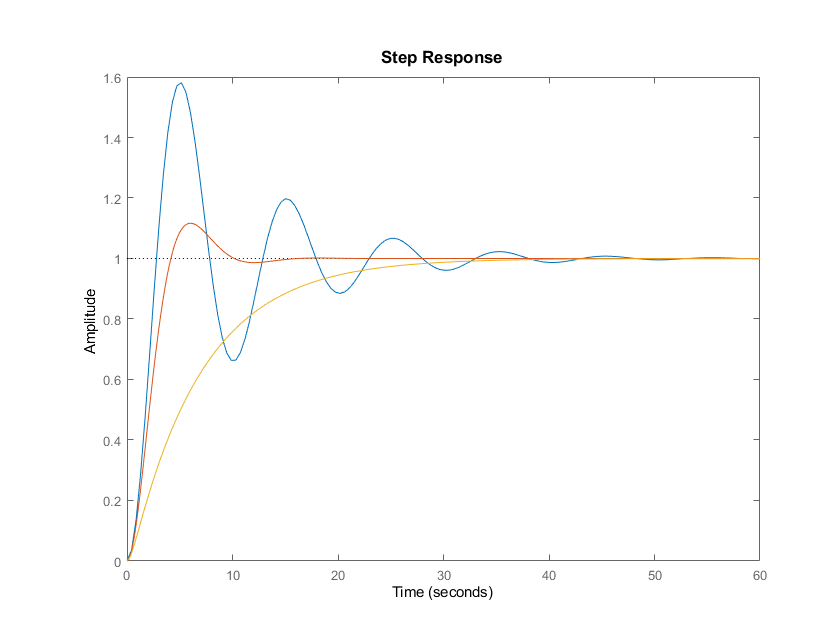

Repeat task 1 above, but to an input force defined by the piecewise function below, using the command lsim(), from $t = 0s$ to $t = 100s$, and plot the result in a new figure.

Hint: typing >> help lsim in MATLAB's command window will guide you on how to use the function.

dt = 0.1;
t = 0:dt:100;
u = t * 0;
for ix=1:length(t)
    if t(ix) < 2.5;
        u(ix) = 0;
    elseif t(ix) <= 9
        u(ix) = 6;
    elseif t(ix) <= 16
        u(ix) = -6;
    else
        u(ix) = 0;   
    end
end
figure()
hold on
for ix = 1:3
zeta = fv(ix) / (M * 2 * wn);    
sys = tf([wn^2], [1 2*zeta*wn wn^2]);
lsim(sys,u,t)
end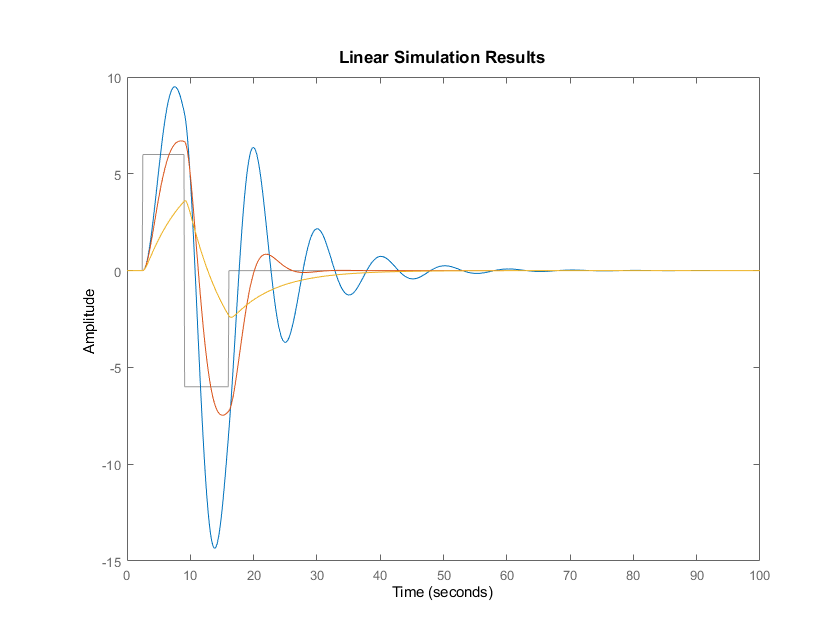

Now, what if we don't know the input function in advance, more specifically, what if the input is a function of the output of the system $f(t,y,y_{\text{sp}})$, as in the case of any feedback control system. In this case we must use a different method to simulate the response. Also note that the methods above require the system to be linear and time-invariant. The next methods can be used to simulate any dynamic system (nonlinear and/or time-variant) if the differential equations and initial conditions are defined.

Given the following differential equation

We can separate it into two equations that can then be used in MATLAB to simulate the response. Let's re-write the equation variables as $x_{1} = x(t),x_{2} = \dot{x}(t),x_{3} = \ddot{x}(t)$. If we define a vector $\mathbf{x}=\begin{bmatrix} x_{1} \\ x_{2} \\ \end{bmatrix}$

then $\dot{\mathbf{x}} = \begin{bmatrix} {\dot{x}}_{1} \\ {\dot{x}}_{2} \\ \end{bmatrix}$

In other words: $\dot{\mathbf{x}} = \begin{bmatrix} {\dot{x}}_{1} \\ {\dot{x}}_{2} \\ \end{bmatrix} = \begin{bmatrix} x_{2} \\ \frac{u\left( t \right) - cx_{1} - bx_{2}}{a} \\ \end{bmatrix}$

If we start off with some given initial conditions for $x_{1},x_{2}$, we can numerically integrate $\dot{\mathbf{x}}$ at consecutive time-steps to obtain

over a given time period $t \in \lbrack 0,t_{f}\rbrack$. In the following code snippet is an example on how to simulate the above equation (3) in MATLAB using ODE45(). ODE45() is MATLAB's Ordinary Differential Equation solver using the Runge-Kutta integration method with a variable time-step for efficient computation.

clear all;
% System Parameters
a = 2;
b = 1;
c = 2;
u = 5; % This is the input, it can also be a variable
 
% Initial Conditions
x0 = [0; 0];
 
% funtion for xdot vector - using an anonymous function. You can also
% define a separate function in a separate file or at the end of the
% script
dxdt = @(t,x) [x(2); (u - b * x(2) - c * x(1)) / a];  
 
%Time vector
t = 0:0.05:20;
 
% Simulate using ODE45
[t_sim, x_sim] = ode45(dxdt,t,x0);
 
% And plot
figure()
plot(t_sim, x_sim)
legend('$x$','$\dot{x}$', 'Interpreter','latex') 
xlabel('Time [s]')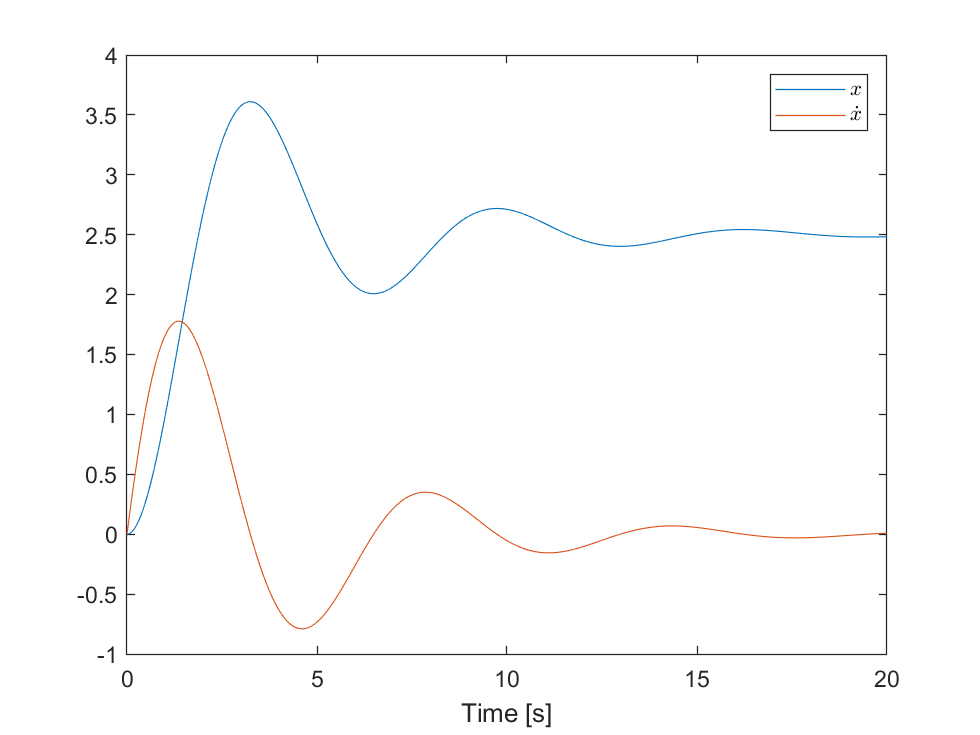

EXERCISE 2

Obtain the differential equation from the transfer function on the first page from equation (1), into the form shown in equation (2), then simulate the response to a sinusoidal input of unity magnitude and $f = 0.1Hz$, $u\left( t \right) = sin(2\pi ft)$, using ODE45(), change the value of the damping coefficient $f_{v}$ to $f_{v} = 0.1\dot{x}$. You now have a nonlinear system. Simulate for $t = \left\lbrack 0,\ 100s \right\rbrack$ and plot both $x,\dot{x}$ on the figure. Note that the differential equation for the spring-mass-damper system above can also be expressed as:

clear all;
% Initial Conditions
x0 = [0; 0];
 
% funtion for xdot vector - using an anonymous function. You can also
% define a separate function in a separate file or at the end of the
% script
M = 7;
K = 2.8;
f = 0.2;
dxdt = @(t,x) [x(2); (sin(2*pi*f*t) - K * x(1) - 0.1 * x(2) * x(2)) / M ];  
 
%Time vector
t = 0:0.01:100;
 
% Simulate using ODE45
[t_sim, x_sim] = ode45(dxdt,t,x0);

% And plot
figure()
plot(t_sim, x_sim)
legend('$x$','$\dot{x}$', 'Interpreter','latex') 
xlabel('Time [s]')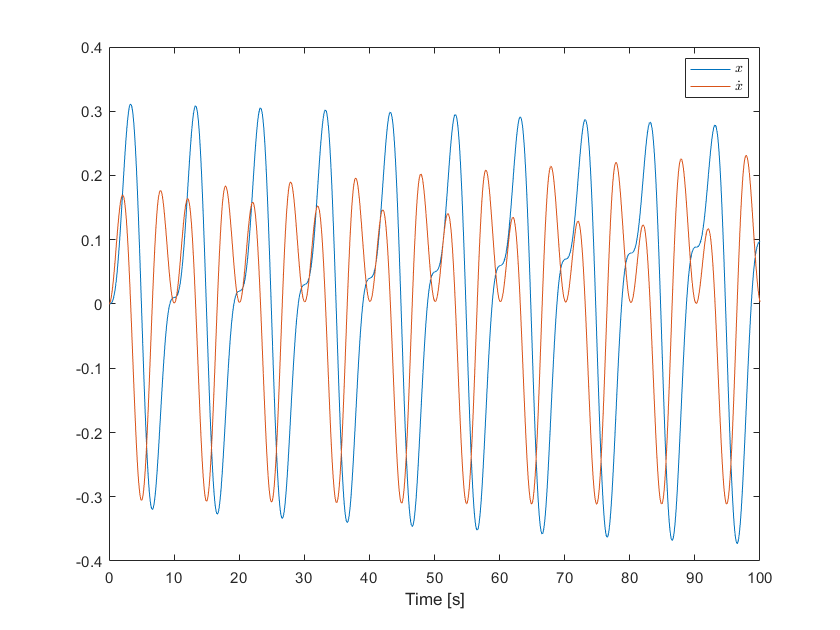

Another method for solving a differential equation is using basic numerical integration with a fixed time-step. This is generally less efficient for higher order systems, but is more flexible in simulating dynamic systems, specifically, in simulating systems in real-time (simulating the dynamics of a car in a video-game is an example). Moreover, this method is sufficient for simulating many mechanical dynamic systems. The code snippet below shows an example of basic forward integration to simulate a second-order system response; the same system from equation (3).

clear all;
% System Parameters
a = 1;
b = 1;
c = 1;
% Initial Conditions
x0 = [0; 0];
 
% funtion for xdot vector - using an anonymous function. You can also
% define a separate function in a separate file or at the end of the
% script
 
dxdt = @(t,x,u_) [x(2); (u_ - b * x(2) - c * x(1)) / a];  
 
% Integration Time step
dt = 0.1;
% Time vector
t = 0:dt:20;
 
% Initialize x
x_sim = zeros(2,length(t)); % Empty 2xn array
u = zeros(1,length(t)); % Empty 1xn vector
x_sim(:,1)= x0;
 

for ix = 1:length(t)-1
    u(1,ix+1) = sin(t(ix)); % Calculate the next input value
    xdot = dxdt(t(ix), x_sim(:,ix), u(1,ix+1)); % Grab the derivative vector
    x_sim(1, ix+1) = x_sim(1, ix) + xdot(1) * dt; % Integrate x1
    x_sim(2, ix+1) = x_sim(2, ix) + xdot(2) * dt; % Integrate x2
end
 
% And plot
figure()
hold on
plot(t,u(1,:))
plot(t,x_sim(1,:))
plot(t,x_sim(2,:))
xlabel('Time [s]')
legend('$u$','$x$','$\dot{x}$', 'Interpreter','latex')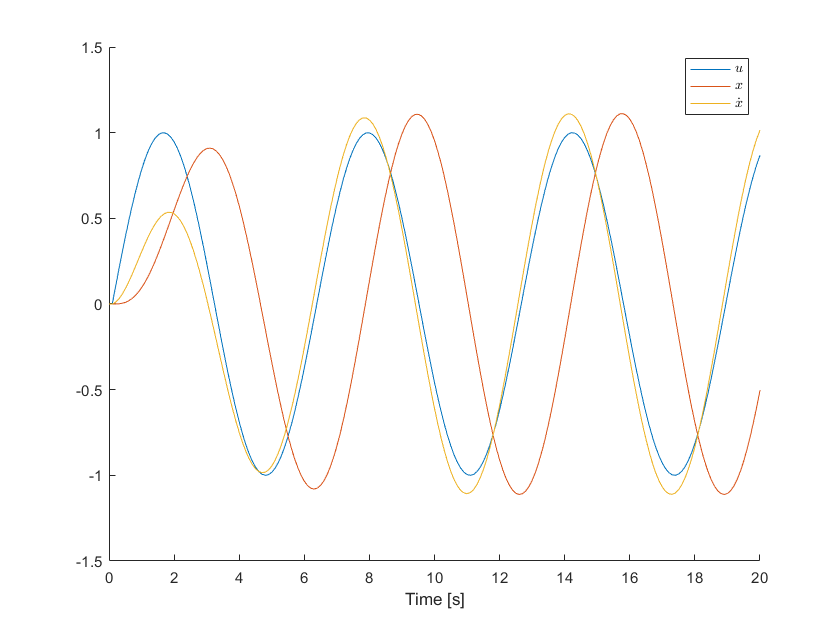

EXERCISE 3

Repeat the previous task ‎3 using basic numerical integration this time, with the following time steps $\Delta t = 0.01$, and $\Delta t = 0.001$. Then plot the responses from the ode45() method and the basic integration method, as three subplots on the same figure. Do you notice a difference in the response between $\Delta t = 0.01s$ and $\Delta t = 0.001s$?

x0 = [0; 0];
M = 7;
K = 2.8;
f = 0.2;
dxdt = @(t,x,u) [x(2); (u  - K * x(1) - 0.1 * x(2) * x(2)) / M ];  
% Integration Time step
dt = 0.01;
% Time vector
t = 0:dt:100;
 
% Initialize x
x_sim = zeros(2,length(t)); % Empty 2xn array
u = zeros(1,length(t)); % Empty 1xn vector
x_sim(:,1)= x0;
 

for ix = 1:length(t)-1
    u(1,ix+1) = sin(2*f*pi*t(ix)); % Calculate the next input value
    xdot = dxdt(t(ix), x_sim(:,ix), u(1,ix+1)); % Grab the derivative vector
    x_sim(1, ix+1) = x_sim(1, ix) + xdot(1) * dt; % Integrate x1
    x_sim(2, ix+1) = x_sim(2, ix) + xdot(2) * dt; % Integrate x2
end
 
% And plot
figure()
hold on
plot(t,u(1,:))
plot(t,x_sim(1,:))
plot(t,x_sim(2,:))
xlabel('Time [s]')
legend('$u$','$x$','$\dot{x}$', 'Interpreter','latex')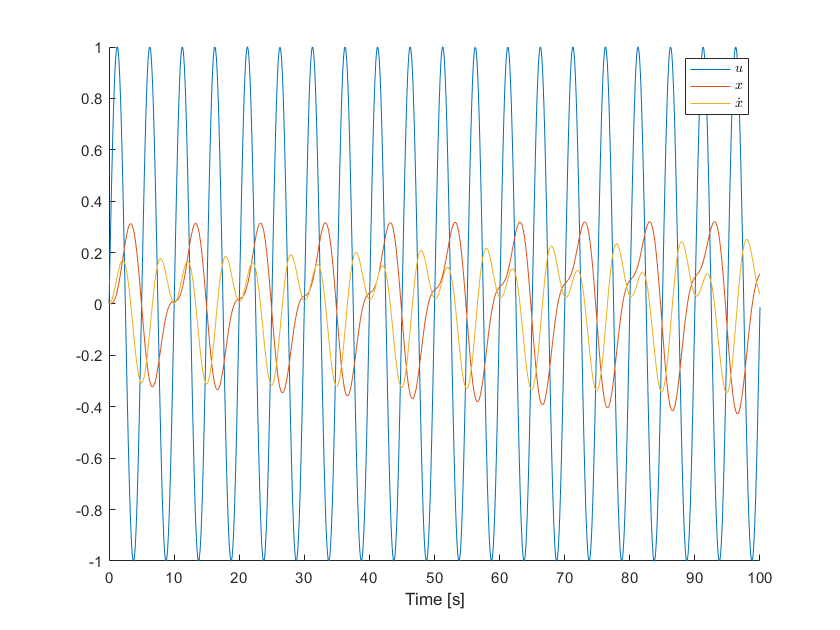

PART II: MODELING & SIMULATING REAL-WORLD SYSTEMS.

Model 1. Satellite Attitude

We wish to model the 2-D attitude of a space satellite body. The 2-D satellite body can be modeled as a rigid-body mass with a moment of inertia $I$, rotating about its center of gravity $\text{C.G.}$ If we neglect the reaction moment from the satellite solar panels attached to the body, the remaining forces acting on the satellite are the thrust forces from the on-board gas thrusters in addition to disturbances that can be modeled as a moment $M_{D}$, as shown on Figure 2.

EXERCISE 4

Given $d = 2m$, $I = 3.5kg \cdot m^{2}$

Derive the equation of motion for the satellite body shown, then derive the transfer function relating the resultant thrust force $F_{R} = F_{1} - F_{2}$ to the angular position of the body $\theta$, that is, find $G\left( s \right) = \frac{\Theta\left( s \right)}{F_{R}\left( s \right)}$. Neglect $M_{D}$. Given the system equation of motion, simulate the response to the following inputs, assuming $M_{D}(t) = 0$. Simulate the response using basic numerical integration.

$F_1 = \begin{cases} 0 & 0 < t < 2s \\ 2 & 2s \leq t < 4s \\ 0 & 4s \leq t \end{cases}$, $F_2 = \begin{cases} 0 & 0 < t < 4s \\ 2 & 4s \leq t < 6s \\ 0 & 6s \leq t \end{cases}$

% Initial Conditions
x0 = [0; 0];
% funtion for xdot vector - using an anonymous function. You can also
% define a separate function in a separate file or at the end of the
% script
I = 3.5;
d = 2;
% Md = 0;
dxdt = @(t,x,u) [x(2); (u * d) / I ];  
% Integration Time step
dt = 0.1;
% Time vector
t = 0:dt:100;
 
% Initialize x
x_sim = zeros(2,length(t)); % Empty 2xn array
u = zeros(1,length(t)); % Empty 1xn vector
for ix=1:length(t)
    if t(ix) < 1
        u(1,ix) = 0;
    elseif t(ix) < 3 
        u(1,ix) = -4;
    elseif t(ix) < 5
        u(1,ix) = 4;
    else
        u(1,ix) = 0;   
    end
end

x_sim(:,1)= x0;
for ix = 1:length(t)-1
    xdot = dxdt(t(ix), x_sim(:,ix), u(1,ix+1)); % Grab the derivative vector
    x_sim(1, ix+1) = x_sim(1, ix) + xdot(1) * dt; % Integrate x1
    x_sim(2, ix+1) = x_sim(2, ix) + xdot(2) * dt; % Integrate x2
end
% And plot
figure()
hold on
plot(t,u(1,:))
plot(t,x_sim(1,:))
plot(t,x_sim(2,:))
xlabel('Time [s]')
legend('$u$','$x$','$\dot{x}$', 'Interpreter','latex')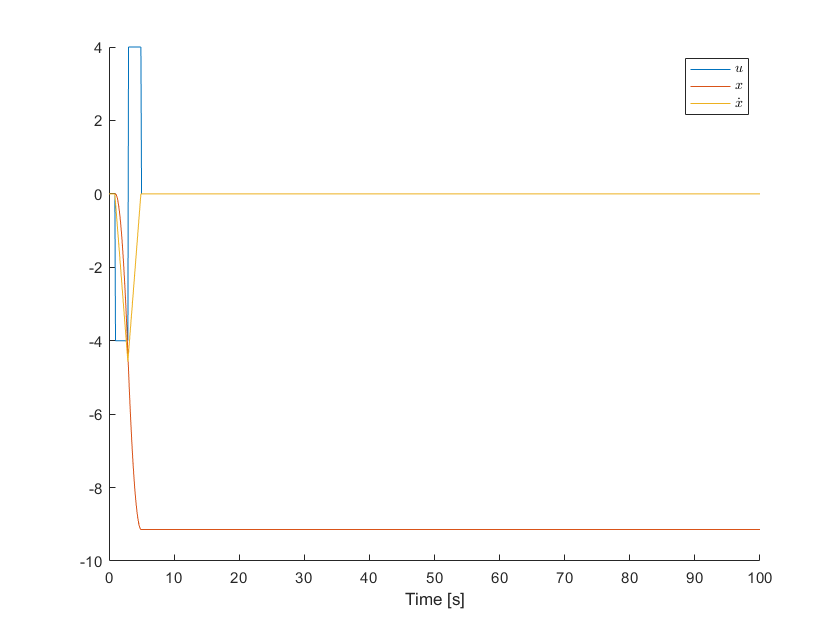

The thruster input function above is termed a bang-bang command. The idea is to apply an equal but opposite set of moments in order to roll the satellite body over a defined angle. The gas thrusters can only act in one direction, so a pair is needed to move-then-stop. This input is termed an open-loop input, meaning it doesn't consider the actual response in the system (it's blind toward the system's actual response). In reality it's quite impossible to control a satellite body in this fashion, we will need to employ a feedback controller to provide just the right amount of thruster force to perform a rotation. Next we will see the effect of adding just a tiny amount of disturbance noise to the model.

Repeat the simulation but this time assume that the disturbance moment is modeled as a zero-mean Gaussian noise with $\sigma = 0.005$. Hint: to generate this random noise value use: $\sigma*randn\left( 1 \right)$

dxdt = @(t,x,u) [x(2); (u * d + 0.005 * randn(1)) / I ];  
% Initialize x
x_sim = zeros(2,length(t)); % Empty 2xn array
x_sim(:,1)= x0;
for ix = 1:length(t)-1
    xdot = dxdt(t(ix), x_sim(:,ix), u(1,ix+1)); % Grab the derivative vector
    x_sim(1, ix+1) = x_sim(1, ix) + xdot(1) * dt; % Integrate x1
    x_sim(2, ix+1) = x_sim(2, ix) + xdot(2) * dt; % Integrate x2
end
% And plot
figure()
hold on
plot(t,u(1,:))
plot(t,x_sim(1,:))
plot(t,x_sim(2,:))
xlabel('Time [s]')
legend('$u$','$x$','$\dot{x}$', 'Interpreter','latex')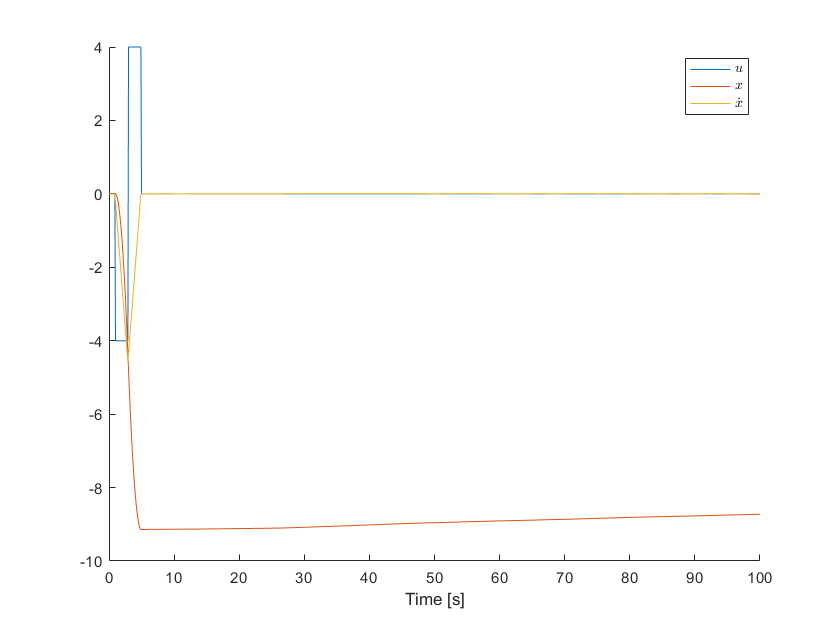

Model 2. Simple Pendulum

A simple pendulum from a uniform slender rod is shown on Figure 3.

The equation of motion for the pendulum is given as

Where $M$ is the torque applied at the pivot, $m_{r}$ is the mass of the rod, $I$ is the rod's moment of inertia about its center of mass, $l$ is the distance from the pivot to the center of mass of the rod and $g$ is the gravity constant

Note that the above equations are nonlinear due to the presence of the trigonometric term $\text{sinθ}$

EXERCISE 5

Given the following parameters:

Simulate the response of the above nonlinear system given the following input function and plot the following responses: $\theta,\dot{\theta}$. Simulate using basic numerical integration. If the response is unstable (grows out of bounds) try to reduce the integration time step $\Delta t$

% System Parameters
clear all;
mr = 3;
l = .19;
I = 4/3*mr*l^2;
g = 9.81;

% Initial Conditions
x0 = [0; 0];
 
% funtion for xdot vector - using an anonymous function. You can also
% define a separate function in a separate file or at the end of the
% script
% Md = 0;
% Integration Time step
dt = 0.001;
% Time vector
t = 0:dt:10;
dxdt = @(t,x,u) [x(2); (u - mr * g * l *sin(x(1))) / ( I + mr * l^2)];  

% Initialize x
x_sim = zeros(2,length(t)); % Empty 2xn array
x_sim(:,1)= x0;
u = zeros(1,length(t)); % Empty 1xn vector
for ix=1:length(t)
    if t(ix) < 3
        u(1,ix) = 5;
    else
        u(1,ix) = 0;   
    end
end

for ix = 1:length(t)-1
    xdot = dxdt(t(ix), x_sim(:,ix), u(1,ix+1)); % Grab the derivative vector
    x_sim(1, ix+1) = x_sim(1, ix) + xdot(1) * dt; % Integrate x1
    x_sim(2, ix+1) = x_sim(2, ix) + xdot(2) * dt; % Integrate x2
end
 
% And plot
figure()
hold on
set(gcf,'Position', [10 10 600 300], 'DefaultLineLineWidth', 2)
plot(t,u(1,:),'k--')
plot(t,x_sim(1,:), 'b:')
plot(t,x_sim(2,:),'r')
grid on
xlabel('Time [s]')
legend('u','x','xdot')  
print(gcf,'foo.png','-dpng','-r600');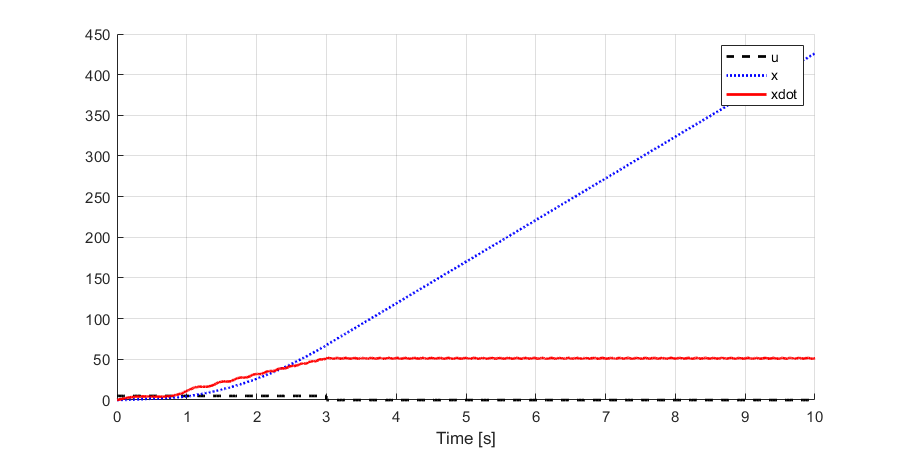

In order to design a controller for this system using the tools we introduce in this course; the system must be linearized. In this case we can linearize the system using the small angle approximation assumption. We can do this because we generally intend to keep (control) the inverted pendulum close to $\theta \approx 0^{o}$.

Linearize the above equations using the small angle approximation. That is, assume $sin\theta = \theta$.

Repeat task ‎1 using the linearized model and compare the nonlinear versus the nonlinear responses, in two subplots, one for each of $\theta,\dot{\theta}$. Briefly explain the observed differences. At what value of $\theta$ does the approximation become noticeably inaccurate?

dxdt = @(t,x,u) [x(2); (u - mr * g * l *(x(1))) / ( I + mr * l^2)];  
for ix = 1:length(t)-1
    xdot = dxdt(t(ix), x_sim(:,ix), u(1,ix+1)); % Grab the derivative vector
    x_sim(1, ix+1) = x_sim(1, ix) + xdot(1) * dt; % Integrate x1
    x_sim(2, ix+1) = x_sim(2, ix) + xdot(2) * dt; % Integrate x2
end
 
% And plot
figure()
hold on
set(gcf,'Position', [10 10 600 300], 'DefaultLineLineWidth', 2)
plot(t,u(1,:),'k--')
plot(t,x_sim(1,:), 'b:')
plot(t,x_sim(2,:),'r')
grid on
xlabel('Time [s]')
legend('u','x','xdot')  
print(gcf,'foo.png','-dpng','-r600');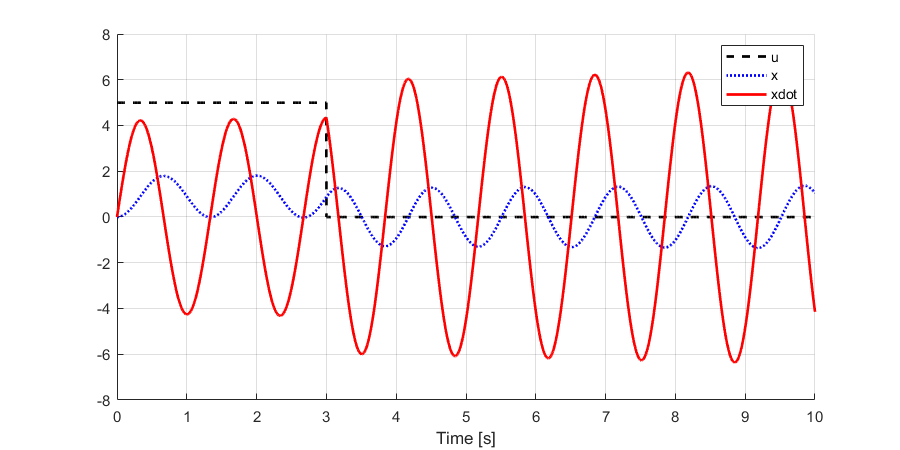

Note that when experimenting with a controller design via simulation, we design the controller using the linearized model if we wish, but it is important to simulate the response as accurate as possible. That is, simulate the nonlinear response.

Explain why it is better to simulate the nonlinear model and not the linearized model, when testing a controller?