ME 417 - Numerical Lesson #3

Back to Lessons

In the first part you will follow a guided example on how to use the Control System Designer app in MATLAB to design a controller using root-locus.

In part two, you will design controllers for the disk drive system from previous assignments, in part four you will design controllers for a DC Motor.

The focus of this lesson is on the design of the controller parameters, you will simulate the response using MATLAB’s built-in functions.

PART I: INTRODUCTION TO CONTROL SYSTEM DESIGNER

A. Disk Drive Time Response Analysis

A disk drive read head can be modeled as a pair of rotating masses connected by a flexible shaft. As shown on Figure 1. $I_{m}$ represents the motor's inertia, while $I_{h}$ represents the head's inertia. The flexible shaft has a stiffness $K$ and damping coefficient $b$. $M_{m}$ is the torque applied by the motor while $M_{D}$ is the disturbance torque.

Given the following system shown on Figure 1, let us first design a proportional controller of the form $G_c =K$ using the Control System Designer, then try to design a controller of the form $G_c =K\frac{s+z}{s+p}$ , where $z$ and $p$ are the zero and pole location of the compensator (controller).

Figure 1

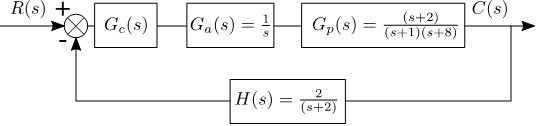
To use the control system designer to design using root-locus only, we call the function controlSystemDesigner() as shown in the following code snippet. Note the block diagram architecture used, which is the default one in Control System Designer app, but it can be changed as well. We will use the standard architecture in this assignment.

%plot inline -f=svg -w 650 -h 400
format compact

s = tf("s");
Gp = (s + 2) / ((s + 1) * (s + 8));
Ga = 1/s;
H = 2 / (s + 2);
Gol = Gp*Ga*H;
% controlSystemDesigner('rlocus',G,C,H,F)
%      r -->[ F ]-->O--->[ C ]--->[ G ]----+---> y
%                 - |                      |
%                   +-------[ H ]----------+

controlSystemDesigner('rlocus',Ga*Gp,1,H,1)  % Comment this out later if you don't want to start the tool

In the code snippet, F is the input filter, it can also be used to scale the unit-step input (say the input r=10, we can place 10 for F). C is the controller transfer function $G_c \left(s\right)$, this can be changed within Control System Designer,. You can leave it as 1 or if you have an idea of the controller you want to use you can add it and then manipulate its parameters inside the tool, in other words the controller $G_c$ can be defined completely within the tool.

$G_a *G_p$ is the equivalent plant transfer function. $G_a$ can represent an actuator that has its own dynamics.

We can alternatively pass the open-loop transfer function to Control System Designer as shown in the following code snippet. But then the tool would not be able to distinguish between the different control block diagram components as we will see next.

controlSystemDesigner('rlocus',Gc*Ga*Gp*H)

I.A – Tuning the gain using the Control System Designer

Let’s see how we can use the Control System Designer tool to select the proper gain value to achieve a given performance specification.

Run the code above, and wait for the app window to show.

Figure 2 shows the main app window.

Figure 2

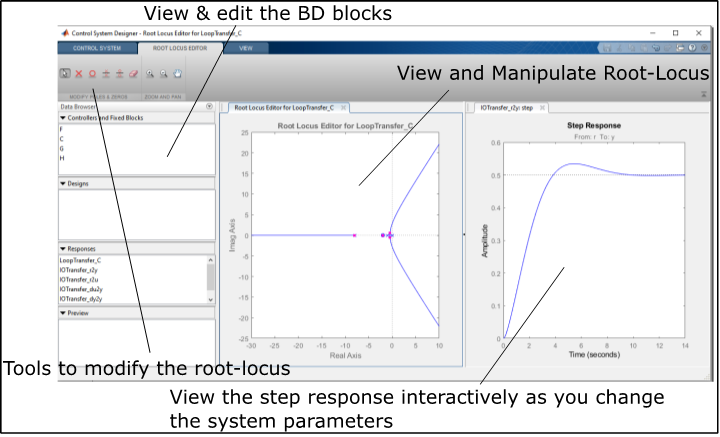
Double click on the C block and change the value to 10, you will notice that the closed loop poles move and the step response is updated to capture the response of the new closed-loop system. As shown on Figure 3

Within the Root-Locus hold and drag one of the closed-loop poles (the purple square). You will notice that they move along the root-locus and the step response updates interactively. This is another way to edit the system and observe the response.

Figure 3

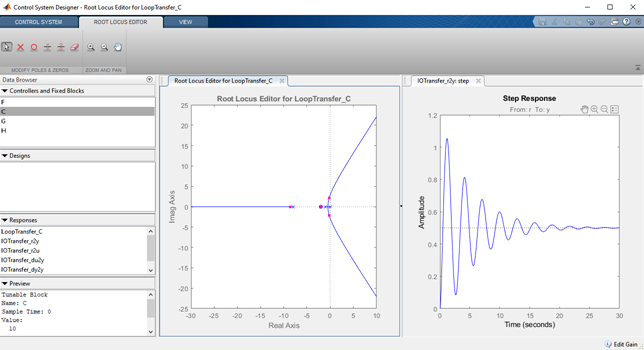
The Control System Designer also allows you to set design targets and observe the time response performance specifications.

-Right click within the Root Locus Editor and select Design Requirements-> New.. , then select Damping Ratio and set the value to be greater than 0.7071 as shown on Figure 4. You will notice a black line is draw that represents the 0.7071 damping ratio line and a shaded area where the damping ratio is higher than 0.7071. The shaded areas represent the lower end of a given performance specifications. As shown on Figure 5

Figure 4

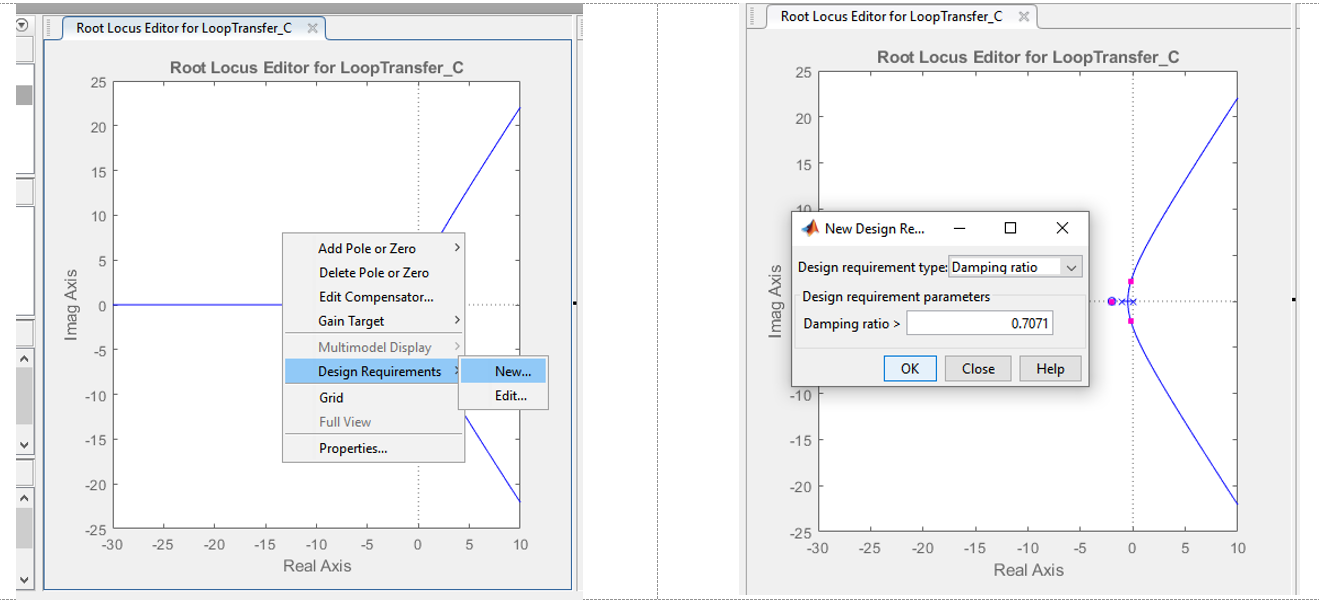
To zoom within the Root Locus Editor, right click within the window, select Properties then change the limits under the limits tap to your desired range.

Figure 5

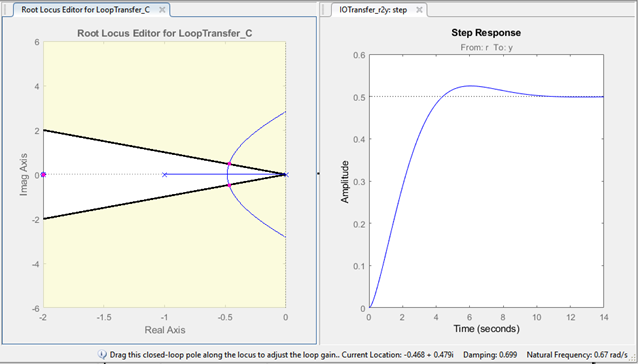
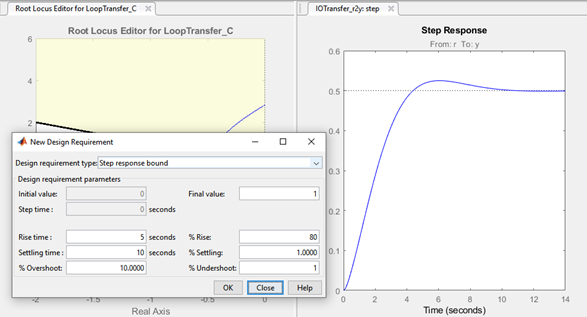
You can set design requirements within the step response window as well. By following the same steps. As shown on Figure 6. The Step Response window will draw black lines and shaded areas to correspond to the design requirements.

Figure 6

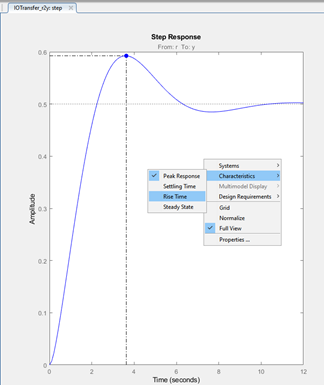
You can also display some of the performance characteristics on the step response window.

-Right click within the step response window. Select Characteristics->Peak Response and the window will highlight the location of the peak response amplitude and time, as shown on Figure 7

Figure 7

EXERCISE 1

Using the above model and Control System Designer, find the value of the controller gain (for the case $G_c =K$), to achieve the following performance specifications:$T_s <10s,T_p <7s,\omega_n >1\frac{rad}{s}$. Use the design requirements tools within the Control System Designer. Show a single view screenshot of your work.

EXERCISE 2

Take the gain value obtained, and simulate the closed-loop response separately in MATLAB using step().

Gc = 2;
Gcl = feedback(Gc*Ga*Gp, H);
figure()
step(Gcl)

I.B – Adding a compensator using the Control System Designer.

If you want to achieve performance specifications that require the closed-loop poles to be placed outside the root-locus using a proportional controller (simple gain), then we would have to change the shape of the root locus by adding a compensator. Let’s see how we can add a compensator of the form $G_c =K\frac{b_1 s+z}{a_1 s+p}$ using the Control System Designer.

Start the Control System Designer using Code Snippet 1. To add a pole or a zero right click within the Root Locus Editor and under Add Pole or Zero, you can find the appropriate selection: An Integrator is a pole at the origin, and a differentiator is a zero at the origin.

EXERCISE 3

Using the above model, design a PD Controller (Ideal Differential Compensator), by placing a zero on the real axis, then choose the gain to achieve the following performance specifications:$T_s <2s, T_p <0.75s,\omega_n >2rad/s$. Use the Control System Designer design requirements aid. Show a screenshot of your work. Note that the PD controller is of the form $G_c {\left(s\right)}=K_p +K_D s=K_D {\left(K_P /K_D +s\right)}$, the zero location will correspond to $-K_P /K_D$, and the gain will equal $K_D$, you can then calculate $K_p$.

Verify by simulating the response of the closed loop system with a PD controller and setting the gains as above, using the step() command.

PART II: DISK DRIVE CONTROL

A disk drive read head can be modeled as a pair of rotating masses connected by a flexible shaft. As shown on Figure 8 Disk Drive Model. }$I_m$ represents the motor’s inertia, while $I_h$ represents the head’s inertia. The flexible shaft has a stiffness $K$ and damping coefficient $b$.$M_m$ is the torque applied by the motor while $M_D$ is the disturbance torque.

Figure 8

With the following parameters given, complete the following problems. Disk Drive Parameters: }$I_m =0\ldotp 1kg\cdot m^2 ,I_h =0\ldotp 04kg\cdot m^2 ,K=0\ldotp 07N\cdot \frac{m}{rad},{\;M}_D \left(t\right)=0,b=0\ldotp 1N\cdot s\cdot \frac{m}{rad}$

II.A Derivation of Transfer Functions

EXERCISE 4

Symbolically derive the transfer functions $G_m {\left(s\right)}=\frac{\theta_m \left(s\right)}{M_m \left(s\right)}$ and $G_h {\left(s\right)}=\frac{\theta_h \left(s\right)}{M_m \left(s\right)}$ in MATLAB. Verify with your answers from the previous assignment

clear all;
I_m_=0.1; I_h_=0.04; K_=0.07; b_=0.1;
syms K b I_m I_h Mm s

A = [I_m*s^2+b*s+K, -b*s-K;
    -b*s-K, I_h*s^2+b*s+K];
B=[1;0];
G_symbolic = inv(A)*B
Gm_s = subs(G_symbolic(1), {K I_m I_h b}, {K_ I_m_ I_h_ b_});
Gh_s = subs(G_symbolic(2), {K I_m I_h b}, {K_ I_m_ I_h_ b_});
[num,den] = numden(Gm_s);
num = sym2poly(num);
den = sym2poly(den);
Gm = tf(num,den)
[num,den] = numden(Gh_s);
num = sym2poly(num);
den = sym2poly(den);
Gh = tf(num,den)

Output:

 
G_symbolic =
 
 (I_h*s^2 + b*s + K)/(I_h*I_m*s^4 + I_h*K*s^2 + I_m*K*s^2 + I_h*b*s^3 + I_m*b*s^3)
           (K + b*s)/(I_h*I_m*s^4 + I_h*K*s^2 + I_m*K*s^2 + I_h*b*s^3 + I_m*b*s^3)
 

Gm =
 
   200 s^2 + 500 s + 350
  ------------------------
  20 s^4 + 70 s^3 + 49 s^2
 
Continuous-time transfer function.


Gh =
 
        500 s + 350
  ------------------------
  20 s^4 + 70 s^3 + 49 s^2
 
Continuous-time transfer function.

 
G_symbolic =
 
 (I_h*s^2 + b*s + K)/(I_h*I_m*s^4 + I_h*K*s^2 + I_m*K*s^2 + I_h*b*s^3 + I_m*b*s^3)
           (K + b*s)/(I_h*I_m*s^4 + I_h*K*s^2 + I_m*K*s^2 + I_h*b*s^3 + I_m*b*s^3)
 

Gm =
 
   200 s^2 + 500 s + 350
  ------------------------
  20 s^4 + 70 s^3 + 49 s^2
 
Continuous-time transfer function.


Gh =
 
        500 s + 350
  ------------------------
  20 s^4 + 70 s^3 + 49 s^2
 
Continuous-time transfer function.

 
G_symbolic =
 
 (I_h*s^2 + b*s + K)/(I_h*I_m*s^4 + I_h*K*s^2 + I_m*K*s^2 + I_h*b*s^3 + I_m*b*s^3)
           (K + b*s)/(I_h*I_m*s^4 + I_h*K*s^2 + I_m*K*s^2 + I_h*b*s^3 + I_m*b*s^3)
 

Gm =
 
   200 s^2 + 500 s + 350
  ------------------------
  20 s^4 + 70 s^3 + 49 s^2
 
Continuous-time transfer function.


Gh =
 
        500 s + 350
  ------------------------
  20 s^4 + 70 s^3 + 49 s^2
 
Continuous-time transfer function.

 
G_symbolic =
 
 (I_h*s^2 + b*s + K)/(I_h*I_m*s^4 + I_h*K*s^2 + I_m*K*s^2 + I_h*b*s^3 + I_m*b*s^3)
           (K + b*s)/(I_h*I_m*s^4 + I_h*K*s^2 + I_m*K*s^2 + I_h*b*s^3 + I_m*b*s^3)
 

Gm =
 
   200 s^2 + 500 s + 350
  ------------------------
  20 s^4 + 70 s^3 + 49 s^2
 
Continuous-time transfer function.


Gh =
 
        500 s + 350
  ------------------------
  20 s^4 + 70 s^3 + 49 s^2
 
Continuous-time transfer function.

 
G_symbolic =
 
 (I_h*s^2 + b*s + K)/(I_h*I_m*s^4 + I_h*K*s^2 + I_m*K*s^2 + I_h*b*s^3 + I_m*b*s^3)
           (K + b*s)/(I_h*I_m*s^4 + I_h*K*s^2 + I_m*K*s^2 + I_h*b*s^3 + I_m*b*s^3)
 

Gm =
 
   200 s^2 + 500 s + 350
  ------------------------
  20 s^4 + 70 s^3 + 49 s^2
 
Continuous-time transfer function.


Gh =
 
        500 s + 350
  ------------------------
  20 s^4 + 70 s^3 + 49 s^2
 
Continuous-time transfer function.

EXERCISE 5

Simulate the closed-loop response again outside the Control System Designer using step(). Structure your plant, controller and closed loop transfer functions. Plot the response of the motor position$\theta_m \left(t\right)$ and head position $\theta_h \left(t\right)$

To get the response of the head, first find the transfer function $\frac{U{\left(s\right)}}{R\left(s\right)}$ where $U(s)$ is the controller output $U\left(s\right)$, given the feedback system block diagram where $G_m$ is the plant transfer function. Then apply this output to the open-loop transfer function $G_h$. This is equivalent to retrieving a record of all the torque actions applied onto the system within feedback, then applying it to the $G_h$ to see how the head position $\theta_h(t)$ responded. See the Error Dynamics Lecture slides for a similar example. Another way to do it is to find the transfer function $\frac{\Theta_h(s)}{\Theta_m(s)}$, then given the motor position response you can directly get the head position. Plot the controller output $u(t)$ in a different subplot.

% controlSystemDesigner('rlocus', Gm)
t = 0:0.001:20;
Kp = .05;
Gc =  Kp;
Gclm = feedback(Gc*Gm, 1)
figure('Position', [0 0 900 450])
step(Gclm, t)
stepinfo(Gclm)
hold on 
step((1-Gclm)*Gc*Gh, t)

Output:

Gclm =
 
           10 s^2 + 25 s + 17.5
  --------------------------------------
  20 s^4 + 70 s^3 + 59 s^2 + 25 s + 17.5
 
Continuous-time transfer function.


ans = 

  <a href="matlab:helpPopup struct" style="font-weight:bold">struct</a> with fields:

        RiseTime: 1.7725
    SettlingTime: 396.0642
     SettlingMin: 0.1166
     SettlingMax: 1.9307
       Overshoot: 93.0653
      Undershoot: 0
            Peak: 1.9307
        PeakTime: 5.3494


Gclm =
 
           10 s^2 + 25 s + 17.5
  --------------------------------------
  20 s^4 + 70 s^3 + 59 s^2 + 25 s + 17.5
 
Continuous-time transfer function.


ans = 

  <a href="matlab:helpPopup struct" style="font-weight:bold">struct</a> with fields:

        RiseTime: 1.7725
    SettlingTime: 396.0642
     SettlingMin: 0.1166
     SettlingMax: 1.9307
       Overshoot: 93.0653
      Undershoot: 0
            Peak: 1.9307
        PeakTime: 5.3494


Gclm =
 
           10 s^2 + 25 s + 17.5
  --------------------------------------
  20 s^4 + 70 s^3 + 59 s^2 + 25 s + 17.5
 
Continuous-time transfer function.


ans = 

  <a href="matlab:helpPopup struct" style="font-weight:bold">struct</a> with fields:

        RiseTime: 1.7725
    SettlingTime: 396.0642
     SettlingMin: 0.1166
     SettlingMax: 1.9307
       Overshoot: 93.0653
      Undershoot: 0
            Peak: 1.9307
        PeakTime: 5.3494

Error using <a href="matlab:matlab.internal.language.introspective.errorDocCallback('DynamicSystem/step', 'C:\Program Files\MATLAB\R2019a\toolbox\shared\controllib\engine\@DynamicSystem\step.m', 95)" style="font-weight:bold">DynamicSystem/step</a> (<a href="matlab: opentoline('C:\Program Files\MATLAB\R2019a\toolbox\shared\controllib\engine\@DynamicSystem\step.m',95,0)">line 95</a>)
"LineWidth" is not a valid plot style.

Error in <a href="matlab:matlab.internal.language.introspective.errorDocCallback('snippet_I2', 'C:\Users\alsai\Dropbox\11_ACADEMIC\02_TEACHING\COURSE_SITES\ME 417 Site\numerical_lessons_matlab\NL3assets\snippet_I2.m', 10)" style="font-weight:bold">snippet_I2</a> (<a href="matlab: opentoline('C:\Users\alsai\Dropbox\11_ACADEMIC\02_TEACHING\COURSE_SITES\ME 417 Site\numerical_lessons_matlab\NL3assets\snippet_I2.m',10,0)">line 10</a>)
step((1-Gclm)*Gc*Gh, t, 'LineWidth', 3)

Error in <a href="matlab:matlab.internal.language.introspective.errorDocCallback('run', 'C:\Program Files\MATLAB\R2019a\toolbox\matlab\lang\run.m', 91)" style="font-weight:bold">run</a> (<a href="matlab: opentoline('C:\Program Files\MATLAB\R2019a\toolbox\matlab\lang\run.m',91,0)">line 91</a>)
evalin('caller', strcat(script, ';'));

Error in <a href="matlab:matlab.internal.language.introspective.errorDocCallback('run_matlab_scripts', 'C:\Users\alsai\Dropbox\11_ACADEMIC\02_TEACHING\COURSE_SITES\ME 417 Site\numerical_lessons_matlab\NL3assets\run_matlab_scripts.m', 21)" style="font-weight:bold">run_matlab_scripts</a> (<a href="matlab: opentoline('C:\Users\alsai\Dropbox\11_ACADEMIC\02_TEACHING\COURSE_SITES\ME 417 Site\numerical_lessons_matlab\NL3assets\run_matlab_scripts.m',21,0)">line 21</a>)
run('snippet_I2.m')


Gclm =
 
           10 s^2 + 25 s + 17.5
  --------------------------------------
  20 s^4 + 70 s^3 + 59 s^2 + 25 s + 17.5
 
Continuous-time transfer function.


ans = 

  <a href="matlab:helpPopup struct" style="font-weight:bold">struct</a> with fields:

        RiseTime: 1.7725
    SettlingTime: 396.0642
     SettlingMin: 0.1166
     SettlingMax: 1.9307
       Overshoot: 93.0653
      Undershoot: 0
            Peak: 1.9307
        PeakTime: 5.3494

Undefined function or variable 'LineWidth'.

Error in <a href="matlab:matlab.internal.language.introspective.errorDocCallback('run_matlab_scripts', 'C:\Users\alsai\Dropbox\11_ACADEMIC\02_TEACHING\COURSE_SITES\ME 417 Site\numerical_lessons_matlab\NL3assets\run_matlab_scripts.m', 22)" style="font-weight:bold">run_matlab_scripts</a> (<a href="matlab: opentoline('C:\Users\alsai\Dropbox\11_ACADEMIC\02_TEACHING\COURSE_SITES\ME 417 Site\numerical_lessons_matlab\NL3assets\run_matlab_scripts.m',22,0)">line 22</a>)
set(findall(gcf,'type','line'),'linewidth',LineWidth);


Gclm =
 
           10 s^2 + 25 s + 17.5
  --------------------------------------
  20 s^4 + 70 s^3 + 59 s^2 + 25 s + 17.5
 
Continuous-time transfer function.


ans = 

  <a href="matlab:helpPopup struct" style="font-weight:bold">struct</a> with fields:

        RiseTime: 1.7725
    SettlingTime: 396.0642
     SettlingMin: 0.1166
     SettlingMax: 1.9307
       Overshoot: 93.0653
      Undershoot: 0
            Peak: 1.9307
        PeakTime: 5.3494


Gclm =
 
           10 s^2 + 25 s + 17.5
  --------------------------------------
  20 s^4 + 70 s^3 + 59 s^2 + 25 s + 17.5
 
Continuous-time transfer function.


ans = 

  <a href="matlab:helpPopup struct" style="font-weight:bold">struct</a> with fields:

        RiseTime: 1.7725
    SettlingTime: 396.0642
     SettlingMin: 0.1166
     SettlingMax: 1.9307
       Overshoot: 93.0653
      Undershoot: 0
            Peak: 1.9307
        PeakTime: 5.3494


Gclm =
 
           10 s^2 + 25 s + 17.5
  --------------------------------------
  20 s^4 + 70 s^3 + 59 s^2 + 25 s + 17.5
 
Continuous-time transfer function.


ans = 

  <a href="matlab:helpPopup struct" style="font-weight:bold">struct</a> with fields:

        RiseTime: 1.7725
    SettlingTime: 396.0642
     SettlingMin: 0.1166
     SettlingMax: 1.9307
       Overshoot: 93.0653
      Undershoot: 0
            Peak: 1.9307
        PeakTime: 5.3494


Gclm =
 
           10 s^2 + 25 s + 17.5
  --------------------------------------
  20 s^4 + 70 s^3 + 59 s^2 + 25 s + 17.5
 
Continuous-time transfer function.


ans = 

  <a href="matlab:helpPopup struct" style="font-weight:bold">struct</a> with fields:

        RiseTime: 1.7725
    SettlingTime: 396.0642
     SettlingMin: 0.1166
     SettlingMax: 1.9307
       Overshoot: 93.0653
      Undershoot: 0
            Peak: 1.9307
        PeakTime: 5.3494


Gclm =
 
           10 s^2 + 25 s + 17.5
  --------------------------------------
  20 s^4 + 70 s^3 + 59 s^2 + 25 s + 17.5
 
Continuous-time transfer function.


ans = 

  <a href="matlab:helpPopup struct" style="font-weight:bold">struct</a> with fields:

        RiseTime: 1.7725
    SettlingTime: 396.0642
     SettlingMin: 0.1166
     SettlingMax: 1.9307
       Overshoot: 93.0653
      Undershoot: 0
            Peak: 1.9307
        PeakTime: 5.3494

II.C Disk Drive Collocated Position Control with Compensation

Going beyond a proportional controller, we can use a compensator to improve the performance of the system even further. In class, we learned about: PI, Lag, PD, Lead, PID and Lead-Lag.

EXERCISE 6

Improve the controller performance by selecting a proper compensator and designing its parameters in the Control System Designer, in order to achieve the following performance specifications: $T_s<1s,\%OS<14\%$. Justify your choice of compensator and provide its parameters.

Simulate the closed-loop system in MATLAB using step(). Plot the responses of the motor and head positions, $\theta_m \left(t\right),\theta_h \left(t\right)$ Plot the controller output $u(t)$, and compare it to the controller output from the previous problem. - Explain the differences. Which one is more aggressive? And which one is more likely to cause issues in real-world implementations and why? Provide a block diagram of your feedback system. (A drawing)

t = 0:0.001:5;
Kp = 3.079*0.22489;
Ki = 0;
Kd = 0.22489;
Gpid = pid(Kp, Ki, Kd)
% Gc =  0.01;
figure('Position', [0 0 900 450])
Gcl = feedback(Gpid*Gm, 1)
E = (1-Gcl)
[e,t] = step(E);
step(Gcl, t)
stepinfo(Gcl)

Output:

Gpid =
 
             
  Kp + Kd * s
             

  with Kp = 0.692, Kd = 0.225
 
Continuous-time PD controller in parallel form.


Gcl =
 
     44.98 s^3 + 250.9 s^2 + 424.9 s + 242.4
  ----------------------------------------------
  20 s^4 + 115 s^3 + 299.9 s^2 + 424.9 s + 242.4
 
Continuous-time transfer function.


E =
 
             20 s^4 + 70 s^3 + 49 s^2
  ----------------------------------------------
  20 s^4 + 115 s^3 + 299.9 s^2 + 424.9 s + 242.4
 
Continuous-time transfer function.


ans = 

  <a href="matlab:helpPopup struct" style="font-weight:bold">struct</a> with fields:

        RiseTime: 0.4331
    SettlingTime: 3.6194
     SettlingMin: 0.9124
     SettlingMax: 1.2866
       Overshoot: 28.6554
      Undershoot: 0
            Peak: 1.2866
        PeakTime: 1.1360


Gpid =
 
             
  Kp + Kd * s
             

  with Kp = 0.692, Kd = 0.225
 
Continuous-time PD controller in parallel form.


Gcl =
 
     44.98 s^3 + 250.9 s^2 + 424.9 s + 242.4
  ----------------------------------------------
  20 s^4 + 115 s^3 + 299.9 s^2 + 424.9 s + 242.4
 
Continuous-time transfer function.


E =
 
             20 s^4 + 70 s^3 + 49 s^2
  ----------------------------------------------
  20 s^4 + 115 s^3 + 299.9 s^2 + 424.9 s + 242.4
 
Continuous-time transfer function.


ans = 

  <a href="matlab:helpPopup struct" style="font-weight:bold">struct</a> with fields:

        RiseTime: 0.4331
    SettlingTime: 3.6194
     SettlingMin: 0.9124
     SettlingMax: 1.2866
       Overshoot: 28.6554
      Undershoot: 0
            Peak: 1.2866
        PeakTime: 1.1360


Gpid =
 
             
  Kp + Kd * s
             

  with Kp = 0.692, Kd = 0.225
 
Continuous-time PD controller in parallel form.


Gcl =
 
     44.98 s^3 + 250.9 s^2 + 424.9 s + 242.4
  ----------------------------------------------
  20 s^4 + 115 s^3 + 299.9 s^2 + 424.9 s + 242.4
 
Continuous-time transfer function.


E =
 
             20 s^4 + 70 s^3 + 49 s^2
  ----------------------------------------------
  20 s^4 + 115 s^3 + 299.9 s^2 + 424.9 s + 242.4
 
Continuous-time transfer function.


ans = 

  <a href="matlab:helpPopup struct" style="font-weight:bold">struct</a> with fields:

        RiseTime: 0.4331
    SettlingTime: 3.6194
     SettlingMin: 0.9124
     SettlingMax: 1.2866
       Overshoot: 28.6554
      Undershoot: 0
            Peak: 1.2866
        PeakTime: 1.1360


Gpid =
 
             
  Kp + Kd * s
             

  with Kp = 0.692, Kd = 0.225
 
Continuous-time PD controller in parallel form.


Gcl =
 
     44.98 s^3 + 250.9 s^2 + 424.9 s + 242.4
  ----------------------------------------------
  20 s^4 + 115 s^3 + 299.9 s^2 + 424.9 s + 242.4
 
Continuous-time transfer function.


E =
 
             20 s^4 + 70 s^3 + 49 s^2
  ----------------------------------------------
  20 s^4 + 115 s^3 + 299.9 s^2 + 424.9 s + 242.4
 
Continuous-time transfer function.


ans = 

  <a href="matlab:helpPopup struct" style="font-weight:bold">struct</a> with fields:

        RiseTime: 0.4331
    SettlingTime: 3.6194
     SettlingMin: 0.9124
     SettlingMax: 1.2866
       Overshoot: 28.6554
      Undershoot: 0
            Peak: 1.2866
        PeakTime: 1.1360


Gpid =
 
             
  Kp + Kd * s
             

  with Kp = 0.692, Kd = 0.225
 
Continuous-time PD controller in parallel form.


Gcl =
 
     44.98 s^3 + 250.9 s^2 + 424.9 s + 242.4
  ----------------------------------------------
  20 s^4 + 115 s^3 + 299.9 s^2 + 424.9 s + 242.4
 
Continuous-time transfer function.


E =
 
             20 s^4 + 70 s^3 + 49 s^2
  ----------------------------------------------
  20 s^4 + 115 s^3 + 299.9 s^2 + 424.9 s + 242.4
 
Continuous-time transfer function.


ans = 

  <a href="matlab:helpPopup struct" style="font-weight:bold">struct</a> with fields:

        RiseTime: 0.4331
    SettlingTime: 3.6194
     SettlingMin: 0.9124
     SettlingMax: 1.2866
       Overshoot: 28.6554
      Undershoot: 0
            Peak: 1.2866
        PeakTime: 1.1360

II.D Disk Drive Non-Collocated Position Control with Compensation

So far we have only attempted to control the motor position with torque applied on the motor. What if our position sensor is not placed on the motor but on the head, and we want to control the position of the head by observing its position (and error) directly, while still acting on the motor. This is called a non-collocated control problem; input and output are not located in the same place.

EXERCISE 7

Design a PID Compensator for the system using Control System Designer to control the head position directly (The open-loop transfer function is now $G_h(s)$). Try to achieve the following performance specifications:$T_s <8s,\%OS<65\%$.

Simulate and plot the responses of $\theta_m(t), \theta_h(t)$ in a subplot and in another. Design your own compensator to achieve the performance specifications. You are not limited to the compensators discussed in class, use your understanding of root-locus manipulate the root-locus by your compensator in such away as to place the root-locus in your design range. Plots the responses of $\theta_m(t),\, \theta_h(t),\, u(t)$ and and explain your choice of compensator. What limitations would your controller have in real-world applications? Provide a block diagram of your feedback system.

PART III: DC MOTOR CONTROL

Given the following DC Motor Model in the Equation shown, with the parameters given. Complete the following tasks. DC Motor Parameters: }$K_t =1Nm/A,K_b =3\frac{Vs}{rad},R_a =10\Omega ,L_a =5H,J=10kgm^2 ,D_m =0\ldotp 5\frac{Nms}{rad}$

III.A DC Motor Velocity Control with Gain Tuning

EXERCISE 8

Using the Control System Designer design a velocity feedback controller for the DC motor, find the value of that achieves (by trial and error) the minimum settling time possible with such a controller. Report the value of $K_p$ achieved and the associated Settling Time $T_s$, Peak Time $T_p$, Percent Overshoot $\%OS$, damping ration $\zeta$, and natural frequency $\omega_n$.

Show a screenshot of your work Simulate the response in MATLAB and plot the velocity response and controller output in separate subplots.

s = tf('s');
Kt = 1; Kb = 3; Ra = 10; La = 5; J = 10; Dm = 0.5;
Gv = Kt * s / ((J * s^2 + Dm * s) * (Ra + La * s) + Kt * Kb *s)

Output:

Gv =
 
             s
  ------------------------
  50 s^3 + 102.5 s^2 + 8 s
 
Continuous-time transfer function.


Gv =
 
             s
  ------------------------
  50 s^3 + 102.5 s^2 + 8 s
 
Continuous-time transfer function.


Gv =
 
             s
  ------------------------
  50 s^3 + 102.5 s^2 + 8 s
 
Continuous-time transfer function.


Gv =
 
             s
  ------------------------
  50 s^3 + 102.5 s^2 + 8 s
 
Continuous-time transfer function.


Gv =
 
             s
  ------------------------
  50 s^3 + 102.5 s^2 + 8 s
 
Continuous-time transfer function.

III.B DC Motor Velocity Control with Compensation

EXERCISE 9

Improve the velocity controller performance by selecting a proper compensator and designing its parameters in the Control System Designer, in order to achieve the following performance specifications:$T_s<0.4s,\%OS<5\%$. Justify your choice of compensator and provide its parameters.

Simulate the closed-loop system in MATLAB using step(). Plot the responses of the motor acceleration and velocity. Plot the controller output $u(t)$, and compare it to the controller output from the previous problem. Can this be practically delivered? Explain.

% controlSystemDesigner('rlocus', Gv)
% 1819.2 (s+0.05) (s+4.671)
%  -------------------------
%       s
Gc = 1819 * (s+0.05) * (s + 4.671) / s;
Gvcl = feedback(Gc*Gv,1);
figure('Position', [0 0 900 450])
step(Gvcl)

Problem III.C DC Motor Position Control with Compensation and Cascade Controllers

For ease of implementation and troubleshooting, it is often more efficient to breakdown the control system design into multiple stages. In this problem you will use the new closed-loop system created from the previous problem and implement a new feedback loop around it to control position. Note that you already have a closed loop system relating reference velocity to output velocity, expressed in terms of the closed-loop transfer function. This can be thought of as a new “plant”, with this new plant we want to apply feedback to control position. The inner velocity control loop and outer position control loops are shown Figure 9, with the equivalent reduced form shown on Figure 10

Figure 9 Figure 10

Practically, this allows the control system designer to tune an inner loop controller to achieve a certain closed-loop response for the inner loop, then step out into the next outer loop and design the outer loop controller etc.

EXERCISE 10

Design a position control outer loop controller, given the closed-loop velocity control transfer function you achieved from the previous problem. Using Control System Designer. Achieve the following performance specifications: $T_s<0.05s, \%OS<2\%$

Justify your choice of controllers, and present your controller parameters.

The velocity control closed-loop transfer function with the integrator and controller $G_2$ is the new open-loop transfer function for the position feedback controller.

Plot the velocity and position response of the motor on one subplot and the output of the position controller on another subplot. What does the output of the position controller represent? Another common example of where cascaded feedback controllers are used is in the control of multi-rotors (i.e. quadrotor drones). The inner loop would be an angular velocities controller that can be tuned (the gyroscope would provide the angular velocities sensing), this inner loop will be tuned, tested and troubleshooted until it produces a satisfactory angular rates response, this new closed-loop will be implemented in an attitude (angular position) controller outer-loop.

Give an example of where cascaded feedback controllers can be used.

% controlSystemDesigner('rlocus', Gvcl/s)
Gc_p = 18;
Gpcl = feedback(Gc_p*Gvcl/s,1);
figure('Position', [0 0 900 450])
step(Gpcl)