ME 417 - Numerical Lesson #4

PART I: FROM S-PLANE PID CONTROLLER DESIGN TO DIGITAL IMPLEMENTATION

Disk Drive System

For the disk drive system shown on Figure 1. In Lesson 2, you've simulated the response to the system using numerical integration and applied a PID controller digitally then tuned it manually. In assignment 3, you've learned how to design the PID controller analytically using the root-locus method. In this lesson, you will take the PID controller you designed in lesson 3 and implement it into the simulation you developed in lesson 2. This is analogous to integrating your controller into a real system.

The catch here, is that the gains $K_{p}$ , $K_{I}$ and $K_{D}$ achieved via root-locus are the continuous domain PID gains, while the gains you implement in the numerical integration method have to be the equivalent discrete gains. In order to convert between the continuous domain PID controller to discrete domain PID controller, you need to use the following discrete PID form:

$u[k]= u[k - 1] + ae[k + be\left\lbrack k - 1 \right\rbrack + ce\lbrack k - 2\rbrack$

Where $a = \left( K_{P} + K_{I}\frac{T_{s}}{2} + \frac{K_{D}}{T_{s}} \right),b = \left( - K_{p} + K_{I}\frac{T_{s}}{2} - \frac{2K_{D}}{T_{s}} \right),c = \frac{K_{D}}{T_{s}}$ ,

$T_{s}$ is the sampling time (the integration time step, $\text{dt}$ , in your numerical integration). The gains $K_{p},K_{I},K_{D}$ are the gains retrieved from the PID controller design in the s-domain (root locus). $u\left\lbrack k - 1 \right\rbrack$ denotes the previous controller output value, $e\lbrack k\rbrack$ is the current error, $e\lbrack k - 1\rbrack$ is the previous error, etc.

Note that, with the discrete controller, we don't integrate or differentiate the error, instead the discrete implementation uses a "difference equation", the integration/differentiation is done implicitly through the gains $a,b,c$

Figure 1 - Disk Drive System

I.A Collocated Control

EXERCISE 1

From the PID gains' values you retrieved in controlling the motor, (Lesson 3 II.C Collocated Control), implement them in a numerical integration simulation of the closed-loop system with PID (which you've completed in lesson 2), while scaling them properly using the difference equation for the control law, in order to control the motor position. Compare your results in the numerical integration simulation with the simulation of the closed-loop response in lesson 3.

Plot the controller output u(t), the motor position $\theta_{m}$ and head position $\theta_{h}$

clear all; 
% Model Parameters
I_m_=0.1; I_h_=0.04; K_=0.07; b_=0.1;
% Model in Impedance Method
syms K b I_m I_h Mm s;
A = [I_m*s^2+b*s+K, -b*s-K;
    -b*s-K, I_h*s^2+b*s+K];
B=[1;0];

% Retrieve the transfer functions from the model
G_symbolic = inv(A)*B;
Gm_s = subs(G_symbolic(1), {K I_m I_h b}, {K_ I_m_ I_h_ b_});
Gh_s = subs(G_symbolic(2), {K I_m I_h b}, {K_ I_m_ I_h_ b_});
[num,den] = numden(Gm_s);
num = sym2poly(num);
den = sym2poly(den);
Gm = tf(num,den);
[num,den] = numden(Gh_s);
num = sym2poly(num);
den = sym2poly(den);
Gh = tf(num,den);

% Simulate using step()
dt = 0.001;
t = 0:dt:5;
Kp = 3.079*0.22489; Ki = 0; Kd = 0.22489;
Gpid = pid(Kp, Ki, Kd);
Gcl = feedback(Gpid*Gm, 1);

% Simulate Using Numerical Integration
dxdt = @(t,x,u) [
    x(2); 
    (u - K_ * x(1) - b_ * x(2) + K_ * x(3) + b_ * x(4)) / I_m_; 
    x(4);
    (-K_ * x(3) - b_ * x(4) + K_ * x(1) + b_ * x(2)) / I_h_ 
    ]; 

% Initialize Simulation Vectors
x = zeros(4, length(t));
u = zeros(1, length(t));
e = zeros(1, length(t));

% Initial Condition - Explicit Declaration
x0 = [0; 0; 0; 0];
x(:,1) = x0;

% Discrete controller gains
Ka = Kp + Ki * dt / 2 + Kd / dt;
Kb = -Kp + Ki * dt / 2 - 2 * Kd / dt;
Kc = Kd/dt;

% Step Input r = 1
r = 1;

% Simulate 
for idx = 1:length(t)
    e(1, idx)   = r - x(1,idx);
    if idx > 2
        u(1,idx) = u(1,idx-1) + Ka*e(1,idx) +Kb*e(1,idx-1) + Kc*e(1,idx-2);
    elseif idx == 2
        u(1,idx) = u(1,idx-1) + Ka*e(1,idx) +Kb*e(1,idx-1);
    elseif idx == 1
        u(1,idx) = Ka*e(1,idx); 
    end
    xdot = dxdt(t(1, idx), x(:,idx), u(1,idx));
    % Integrate state
    if(idx < length(t))
        x(:,idx+1) = x(:,idx) + xdot*dt;
    end
end

%% BLOTTING
%plot inline --format=svg
%plot inline -s 900,450
%plot inline -r 120
figure();
[xstep, tstep] = step(Gcl, t);
plot(tstep,xstep, 'k:', 'LineWidth', 2)
hold on
plot(t(1,1:end),x(1,1:end), 'r:', 'LineWidth', 3)
legend (["Step", "Numerical Integration"])
grid on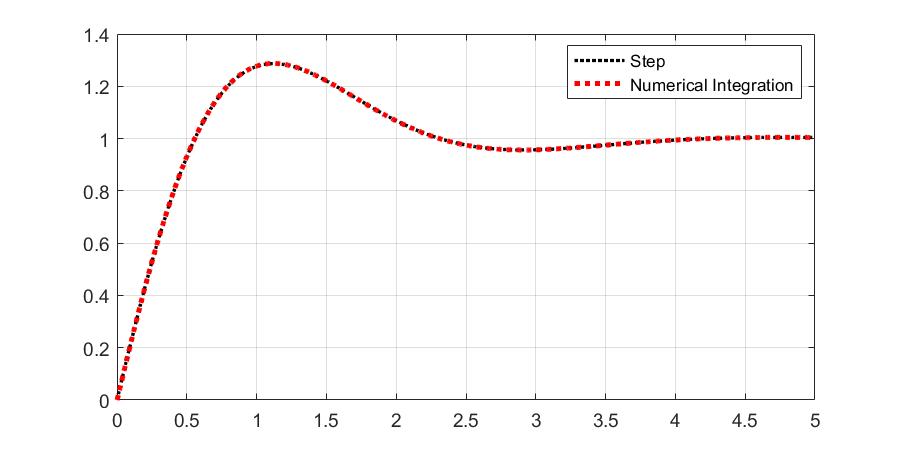

I.B Non-Collocated Control

EXERCISE 2

Repeat the process in I.A, but this time for the non-collocated control problem.

Note that the error is $e = r - \theta_{h}$
Plot the controller output u(t), the motor position $\theta_{m}$ and head position $\theta_{h}$

% Simulate using step()
dt = 0.01;
t = 0:dt:5;
Kp = 0.25; Ki = 0; Kd = 0.8;
Gpid = pid(Kp, Ki, Kd);
Gcl = feedback(Gpid*Gh, 1); % Feedback around head not motor

% Simulate Using Numerical Integration
dxdt = @(t,x,u) [
    x(2); 
    (u - K_ * x(1) - b_ * x(2) + K_ * x(3) + b_ * x(4)) / I_m_; 
    x(4);
    (-K_ * x(3) - b_ * x(4) + K_ * x(1) + b_ * x(2)) / I_h_ 
    ]; 

% Initialize Simulation Vectors
x = zeros(4, length(t));
u = zeros(1, length(t));
e = zeros(1, length(t));

% Initial Condition - Explicit Declaration
x0 = [0; 0; 0; 0];
x(:,1) = x0;

% Discrete controller gains
Ka = Kp + Ki * dt / 2 + Kd / dt;
Kb = -Kp + Ki * dt / 2 - 2 * Kd / dt;
Kc = Kd/dt;

% Step Input r = 1
r = 1;

% Simulate 
for idx = 1:length(t)
    e(1, idx)   = r - x(3,idx); % Change output being fed-back, everything else remains the same
    if idx > 2
        u(1,idx) = u(1,idx-1) + Ka*e(1,idx) +Kb*e(1,idx-1) + Kc*e(1,idx-2);
    elseif idx == 2
        u(1,idx) = u(1,idx-1) + Ka*e(1,idx) +Kb*e(1,idx-1);
    elseif idx == 1
        u(1,idx) = Ka*e(1,idx); 
    end
    xdot = dxdt(t(1, idx), x(:,idx), u(1,idx));
    % Integrate state
    if(idx < length(t))
        x(:,idx+1) = x(:,idx) + xdot*dt;
    end
end

%% BLOTTING
%plot inline --format=svg
%plot inline -s 900,450
%plot inline -r 120
figure();
[xstep, tstep] = step(Gcl, t);
plot(tstep,xstep, 'k:', 'LineWidth', 2)
hold on
plot(t(1,1:end),x(3,1:end), 'r:', 'LineWidth', 3)
legend (["Step", "Numerical Integration"])
grid on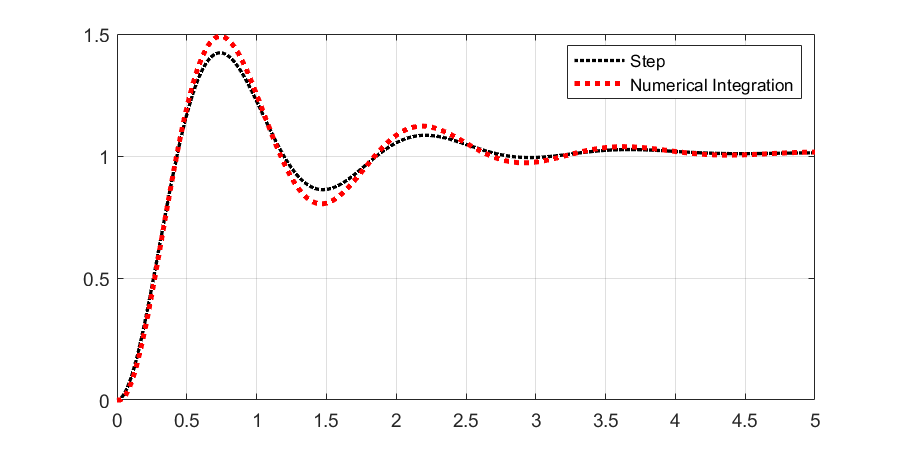

In this example, the numerical integration differs from the continous domain solution, can you guess why? Decrease $dt$ and retry.

PART II: MULTIPLE OUTPUT CONTROLLER DESIGN FOR A STABLE NONLINEAR SYSTEM

Bridge Crane System

A bridge crane is modeled as a cart suspended on a rail with a pendulum connected to the cart, as shown on Figure 2.

Figure 2 - Hanging Crane

The equations of motion for the crane model above is given by the following

\left( m_{c} + m_{r} \right)\ddot{x} + b\dot{x} + m_{r}l\ddot{\theta}cos\theta - m_{r}l{\dot{\theta}}^{2}sin\theta = f(t) \left( I + m_{r}l^{2} \right)\ddot{\theta} + m_{r}glsin\theta = - m_{r}l\ddot{x}\text{cosθ}

After algebraic manipulation to remove the coupling of second derivates, we get

\begin{aligned} \left( \left( I + m_{r}l^{2} \right)\left( m_{c} + m_{r} \right) - m_{r}^{2}l^{2}\cos^{2}\theta \right)\ddot{x} - \left( I + m_{r}l^{2} \right)m_{r}l{\dot{\theta}}^{2}cos\theta - m_{r}^{2}l^{2}gcos\theta sin\theta + \left( I + m_{r}l^{2} \right)b\dot{x} = \left( I + m_{r}l^{2} \right)f(t) \\ \left( \left( m_{r} + m_{c} \right)\left( I + m_{r}l^{2} \right) - m_{r}^{2}l^{2}\cos^{2}\theta \right)\ddot{\theta} - b\dot{x} + m_{r}\text{lcosθ}{\dot{\theta}}^{2} + \left( m_{r} + m_{c} \right)m_{r}glsin\theta = - m_{r}lcos\theta f(t) \end{aligned}

Where $b$ is the coefficient of friction between the wheels and the track, $m_{r}$ and $m_{c}$ are the rod and cart mass respectively, $I$ is the rod's moment of inertia about its center of mass, $l$ is the distance from the pivot to the center of mass of the rod and $g$ is the gravity constant. Note that the above equations are nonlinear due to the presence of the trigonometric terms $sin\theta,\, cos\theta$ and the square term ${\dot{\theta}}^{2}$ .

Given the following parameters:

Parameter	$m_{c}$	$m_{r}$	$I$	$l$	$b$
Value	$10kg$	$2kg$	$0.11kg \cdot m^{2}$	$40cm$	$20N - \text{/}m$

II.A Linearizing, Modeling in State-Space Form and Converting to Transfer Function

EXERCISE 3

Linearize the crane model above from equations above and construct the state-space representation of the system. Provide your answer within the MATLAB script. Construct your output vector as $y = \begin{bmatrix} x \\ \theta \\ \end{bmatrix} = \begin{bmatrix} x_{1} \\ x_{3} \\ \end{bmatrix}$

To linearize: assume the following approximations: $sin\theta \approx \theta,cos\theta \approx 1,{\dot{\theta}}^{2} \approx 0$

clear all;
mr = 2; mc = 10; I = 0.106; b = 20; l = .4; g = 9.81;

Den = ((I + mr*l^2) * (mc + mr) - mr^2 * l^2);

A = [
    0, 1, 0, 0;
    0, -(I + mr*l^2)*b/Den, +mr^2*l^2*g/Den, 0; 
    0, 0, 0, 1;
    0, b/Den, -(mr + mc)*mr*g*l, 0
    ];
B = [0; (I + mr*l^2)/Den; 0; -mr*l/Den];
C = [1 0 0 0; 0 0 1 0];
D = [0; 0];

EXERCISE 4

Using the state-space model, derive the transfer functions relating the input $f(t)$ to cart position $x(t)$ : $G_{1}\left( s \right) = \frac{X(s)}{F(s)}$ , and input $f(t)$ to payload angle $\theta(t)$ : $G_{2}\left( s \right) = \frac{\Theta(s)}{F(s)}$

You can use the MATLAB built-in function $ss2ft()$ , or
Use $G(s)\mathbf{= C}\frac{adj(s\mathbf{I} - \mathbf{A})}{det(s\mathbf{I} - \mathbf{A})}\mathbf{B}$

Note that since $C\mathcal{\in R}^{2 \times 1}$ , there would be two transfer functions corresponding to the two outputs.

[num,den] = ss2tf(A,B,C,D);
Gcart = tf(num(1,:),den)
Gpendulum = tf(num(2,:),den)

Gcart =
     
               0.09526 s^2 + 8.72
      -------------------------------------
      s^4 + 1.905 s^3 + 94.18 s^2 + 173.1 s
    
    Continuous-time transfer function.    
    
Gpendulum =   
       -0.1789 s^2 + 0.08521 s - 1.495e-15
      -------------------------------------
      s^4 + 1.905 s^3 + 94.18 s^2 + 173.1 s

    Continuous-time transfer function.

II.B Cart-Only Position Control and Disturbance Rejection via PID Control

EXERCISE 5

Given the transfer function relating the input to cart position, $G_{1}(s)$ , design a controller to control the cart position.

Implement your designed controller in the crane simulation provided for a step input $r\left( t \right) = 4m$

Plot the position variables $x,\theta$ in one subplot, the velocity variables $\dot{x},\dot{\theta}$ in another subplot, and the output $u(t)$ in the third subplot.

%CRANE 

% Simulate using step()
dt = 0.0001;
t = 0:dt:10;
Kp = 200; Ki = 50; Kd = 100;
Gpid = pid(Kp, Ki, Kd);
Gcl = feedback(Gpid*Gcart, 1); % Feedback around head not motor

% Simulate Using Numerical Integration
dxdt = @(t,x,u) [
    x(2);
    ((I + mr*l^2) * u + (I + mr*l^2)*mr*l*x(4)^2*cos(x(3)) + mr^2*l^2*g*cos(x(3))*sin(x(3))...
    - (I + mr*l^2)*b*x(2)) / ((I + mr*l^2)*(mc + mr) - mr^2*l^2*cos(x(3))^2);
    x(4);  
    (b*x(2) - mr*l*cos(x(3))*x(4)^2 - (mr + mc)*mr*g*l*sin(x(3)) - mr * l * cos(x(3))* u) /...
    ((I + mr*l^2)*(mc + mr) - mr^2*l^2*cos(x(3))^2) 
    ];

% Initialize Simulation Vectors
x = zeros(4, length(t));
u = zeros(1, length(t));
e = zeros(1, length(t));

% Initial Condition - Explicit Declaration
x0 = [0; 0; 0; 0];
x(:,1) = x0;

% Discrete controller gains
Ka = Kp + Ki * dt / 2 + Kd / dt;
Kb = -Kp + Ki * dt / 2 - 2 * Kd / dt;
Kc = Kd/dt;

% Step Input r = 4
r = 4;

% Simulate 
for idx = 1:length(t)
    e(1, idx)   = r - x(1,idx);
    if idx > 2
        u(1,idx) = u(1,idx-1) + Ka*e(1,idx) +Kb*e(1,idx-1) + Kc*e(1,idx-2);
    elseif idx == 2
        u(1,idx) = u(1,idx-1) + Ka*e(1,idx) +Kb*e(1,idx-1);
    elseif idx == 1
        u(1,idx) = Ka*e(1,idx); 
    end
    xdot = dxdt(t(1, idx), x(:,idx), u(1,idx));
    % Integrate state
    if(idx < length(t))
        x(:,idx+1) = x(:,idx) + xdot*dt;
    end
end

%% BLOTTING
%plot inline --format=svg
%plot inline -s 900,450
%plot inline -r 120
figure();
[xstep, tstep] = step(4*Gcl, t);
plot(tstep,xstep, 'k:', 'LineWidth', 2)
hold on
plot(t(1,1:end),x(1,1:end), 'r', 'LineWidth', 1)
legend (["Step", "Numerical Integration"])
grid on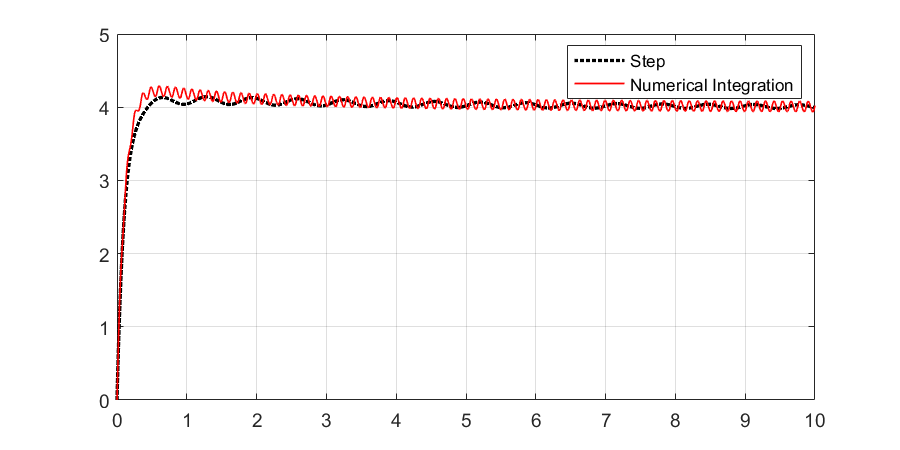

The numerical integration simulation has a different response, can you guess why? Are the models the same?

EXERCISE 6

Create a new model of the crane which includes a small random disturbance in the input, then apply it in the simulation and test your controller performance again.

Here the input inside the simulation would be $u = u_{c} + \omega$ , where $u_{c}$ is the output of the controller and $\omega$ is the disturbance noise.
The disturbance $\omega$ , should be a zero-mean, normally distributed noise with $\sigma = 500$ .
You can choose to emulate a single direction noise – as if wind was blowing on the crane/payload.

Plot the position variables $x,\theta$ in one subplot, the velocity variables $\dot{x},\dot{\theta}$ in another subplot, and the output $u(t)$ in the third subplot.

dxdt_noisy = @(t,x,u) [
    x(2);
    ((I + mr*l^2) * (u+500*randn()) + (I + mr*l^2)*mr*l*x(4)^2*cos(x(3)) + mr^2*l^2*g*cos(x(3))*sin(x(3)) - (I + mr*l^2)*b*x(2)) /...
    ((I + mr*l^2)*(mc + mr) - mr^2*l^2*cos(x(3))^2);
    x(4);  
    (b*x(2) - mr*l*cos(x(3))*x(4)^2 - (mr + mc)*mr*g*l*sin(x(3)) - mr * l * cos(x(3))* (u+500*randn())) / ((I + mr*l^2)*(mc + mr) ...
    - mr^2*l^2*cos(x(3))^2) 
    ];

% Initialize Simulation Vectors
xnoisy = zeros(4, length(t));
u = zeros(1, length(t));
e = zeros(1, length(t));

% Initial Condition - Explicit Declaration
x0 = [0; 0; 0; 0];
xnoisy(:,1) = x0;

% Discrete controller gains
Ka = Kp + Ki * dt / 2 + Kd / dt;
Kb = -Kp + Ki * dt / 2 - 2 * Kd / dt;
Kc = Kd/dt;

% Step Input r = 4
r = 4;

% Simulate 
for idx = 1:length(t)
    e(1, idx)   = r - xnoisy(1,idx);
    if idx > 2
        u(1,idx) = u(1,idx-1) + Ka*e(1,idx) +Kb*e(1,idx-1) + Kc*e(1,idx-2);
    elseif idx == 2
        u(1,idx) = u(1,idx-1) + Ka*e(1,idx) +Kb*e(1,idx-1);
    elseif idx == 1
        u(1,idx) = Ka*e(1,idx); 
    end
    xdot = dxdt_noisy(t(1, idx), xnoisy(:,idx), u(1,idx));
    % Integrate state
    if(idx < length(t))
        xnoisy(:,idx+1) = xnoisy(:,idx) + xdot*dt;
    end
end

%% BLOTTING
%plot inline --format=svg
%plot inline -s 900,450
%plot inline -r 120
figure();
plot(t(1,1:end),x(1,1:end), 'r', 'LineWidth', 1)
hold on
grid on
plot(t(1,1:end),xnoisy(1,1:end), 'k:', 'LineWidth', 1.5)
legend (["Ideal", "Noisy"])
xlabel("Time [s]"); ylabel("Position [m]"); title("Cart Position Response")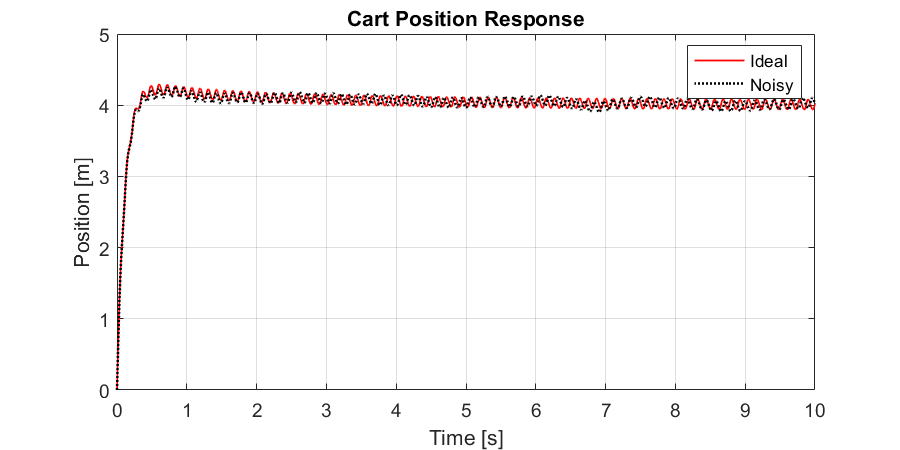

II.C Payload-Only Position Control and Disturbance Rejection via PID Control

EXERCISE 7

Repeat the same steps in II.B, but this time design your controller around $G_{2}(s)$ , the transfer function relating the input to the payload angle position.

Given the transfer function relating the input to payload angular position, $G_{2}(s)$ , implement a regulator to control the payload angle.

Implement your designed controller in the crane simulation provided, without disturbance, for a step input $r\left( t \right) = 0rad\text{/}s$ but change the initial condition s.t. $\theta_{0} = \pi\text{/}2$ , this is analogous to holding the payload at an angle, then releasing it and having the controller bring the position $\theta$ to zero, hopefully faster than it would on its own.

Plot the position variables $x,\theta$ in one subplot, the velocity variables $\dot{x},\dot{\theta}$ in another subplot, and the output $u(t)$ in the third subplot. Simulate the response with and without disturance.

% Initialize Simulation Vectors
x = zeros(4, length(t));
xnoisy = zeros(4, length(t));
u = zeros(1, length(t));
unoisy = zeros(1, length(t));
e = zeros(1, length(t));
enoisy = zeros(1, length(t));

% Initial Condition - Explicit Declaration
x0 = [0; 0; 1.5; 0];
xnoisy(:,1) = x0;
x(:,1) = x0;

Kp = -4.9; Ki = 0; Kd = -8.5;

% Discrete controller gains
Ka = Kp + Ki * dt / 2 + Kd / dt;
Kb = -Kp + Ki * dt / 2 - 2 * Kd / dt;
Kc = Kd/dt;

% Step Input r = 0
r = 0;

% Simulate 
for idx = 1:length(t)
    e(1, idx)   = r - x(3,idx);
    enoisy(1, idx)   = r - xnoisy(3,idx);
    
    if idx > 2
        u(1,idx) = u(1,idx-1) + Ka*e(1,idx) +Kb*e(1,idx-1) + Kc*e(1,idx-2);
        unoisy(1,idx) = unoisy(1,idx-1) + Ka*enoisy(1,idx) +Kb*enoisy(1,idx-1) + Kc*enoisy(1,idx-2);
    elseif idx == 2
        u(1,idx) = u(1,idx-1) + Ka*e(1,idx) +Kb*e(1,idx-1);
        unoisy(1,idx) = unoisy(1,idx-1) + Ka*enoisy(1,idx) +Kb*enoisy(1,idx-1);
    elseif idx == 1
        u(1,idx) = Ka*e(1,idx);
        unoisy(1,idx) = Ka*enoisy(1,idx);
    end
    xdot = dxdt(t(1, idx), x(:,idx), u(1,idx));
    xdot_noisy = dxdt_noisy(t(1, idx), xnoisy(:,idx), unoisy(1,idx));
    
    % Integrate state
    if(idx < length(t))
        x(:,idx+1) = x(:,idx) + xdot*dt;
        xnoisy(:,idx+1) = xnoisy(:,idx) + xdot_noisy*dt;
    end
end

%% BLOTTING
%plot inline --format=svg
%plot inline -s 900,450
%plot inline -r 120
figure();
plot(t(1,1:end),x(3,1:end), 'r', 'LineWidth', 1)
hold on
grid on
plot(t(1,1:end),xnoisy(3,1:end), 'k:', 'LineWidth', 1.5)
legend (["Ideal", "Noisy"])
xlabel("Time [s]"); ylabel("Angle [$\theta$]",'Interpreter','latex'); title("Payload Response")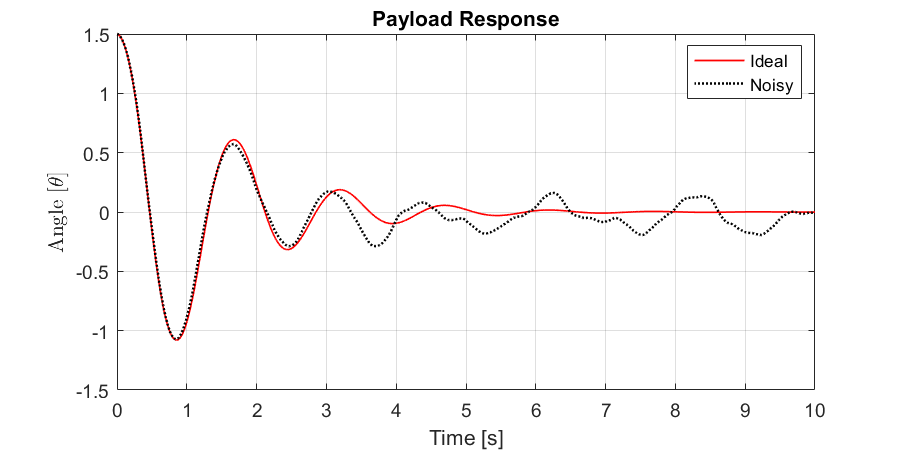

II.D Crane Control via Full State Feedback

Note that you were only able to control either the cart position or the payload position with the transfer function / root-locus design approach above. We can, instead, apply a full state feedback controller if we wish to "attack" and stabilize multiple states/outputs simultaneously.

Given the open-loop state-space model of a system

\dot{\mathbf{x}}\mathbf{=}\mathbf{A}\mathbf{x +}\mathbf{B}u,\, u\mathbf{\in}\mathcal{R}^{1}

\mathbf{y \in}\mathcal{R}^{1}\mathbf{=}\mathbf{C}\mathbf{x}

If we define our controller output as $u = r - \mathbf{\text{Kx}}$ , which is the state feedback controller output, then the closed-loop state-space system becomes:

\dot{\mathbf{x}}\mathbf{= Ax + B}\left( \mathbf{r - Kx} \right)\mathbf{=}\left( \mathbf{A - BK}\right)\mathbf{x + Br}

\mathbf{y = Cx}

Remembering that the poles of the closed-loop system are the eigenvalues of the system matrix $\left( \mathbf{A - BK} \right)\mathbf{,}$ in which the characteristic polynomial of the closed-loop system $= det\left( \mathbf{A - BK} \right)\mathbf{= 0}$

Knowing we have $n = 4$ states, the characteristic polynomial of the system is of the form

p\left( s \right) = a_{4}s^{4} + a_{3}s^{3} + a_{2}s^{2} + a_{1}s + a_{0} = 0

If we wish that the system exhibits a specific transient response, we can then choose the location of our $n$ poles to achieve this response, then match the values of the gain matrix $\mathbf{K}$ to the coefficients of the polynomial $p(s)$ , then use those calculated gains in our controller.

With full state feedback, the controller is function of a weighted average of all the system states, unlike the PID Controller which is a function of the error between the reference and a single output.

EXERCISE 8

Given the state-space model of the system, define the $n = 4$ pole locations in the s-plane, then use the MATLAB built-in command $place()$ , to compute the gain matrix $\mathbf{K} \in \mathcal{R}^{4 \times 1}$ .

It helps to first observe the root-locus shape from PART III.A, then reasonably judge where you would want to place the dominant complex poles and the additional two poles.

Simulate the response of the system using lsim(), with $r = 0$ and the initial condition $x_{0} = \begin{bmatrix} 0 & 0 & \pi\text{/}4 & 0 \\ \end{bmatrix}^{T}$ . Through trial and error, repeat tasks 1 and 2 until you achieve a settling time for both the payload angle and cart position of $T_{s} < 5s$ (the payload reaches $\theta \approx 0rad$ and cart reaches $x \approx 0m$ as well, in under 5s)

Note that you can use the MATLAB function $ss()$ to build a MATLAB dynamic system from the state-space matrices.
Note that for the closed-loop system your " $\mathbf{A}$ " matrix is $(\mathbf{A} - \mathbf{B}\mathbf{K})$ , where $\mathbf{K}$ is the gain matrix calculated in task 1.

Plot the position variables $x,\theta$ in one subplot, the velocity variables $\dot{x},\dot{\theta}$ in another subplot.

Implement your controller in the crane simulation provided, with and without disturbance.

Note that you will need to replace the PID controller with the state feedback controller $u = r - \mathbf{K}x$

Looks like magic? Well, in real-world systems it is often not practical, if even possible, to measure all the states of the system. But instead, we can implement a state observer to "estimate" the states of the system from the available measurements. Conceptually, an observer is analogous to running a model in reverse: if we can see a few $m$ outputs, and know the input to the system $u$ , then what were the $n$ states that "could have" caused this output?

p1 = -2+10i;
p2 = -2-10i;
p3 = -5;
p4 = -6;
K = place(A,B,[p1 p2 p3 p4]);
sys_cl = ss(A-B*K,B,C,0);


r = t*0;
x0 = [0; 0; 1.5; 0];
[xlsim,tlsim] = lsim(sys_cl,r,t,x0);

% Initialize Simulation Vectors
x = zeros(4, length(t));
xnoisy = zeros(4, length(t));
u = zeros(1, length(t));
unoisy = zeros(1, length(t));
e = zeros(1, length(t));
enoisy = zeros(1, length(t));

% Initial Condition - Explicit Declaration
x(:,1) = x0;
xnoisy(:,1) = x0;

Kp = -0.7; Ki = 0; Kd = -70;

% Discrete controller gains
Ka = Kp + Ki * dt / 2 + Kd / dt;
Kb = -Kp + Ki * dt / 2 - 2 * Kd / dt;
Kc = Kd/dt;

% Step Input r = 0
r = 0;

% Simulate 
for idx = 1:length(t)

    u(1, idx) = r - K*x(:,idx);
    unoisy(1, idx) = r - K*xnoisy(:,idx);
    
    xdot = dxdt(t(1, idx), x(:,idx), u(1,idx));
    xdot_noisy = dxdt_noisy(t(1, idx), xnoisy(:,idx), unoisy(1,idx));
    
    % Integrate state
    if(idx < length(t))
        x(:,idx+1) = x(:,idx) + xdot*dt;
        xnoisy(:,idx+1) = xnoisy(:,idx) + xdot_noisy*dt;
    end
end

%% BLOTTING
%plot inline --format=svg
%plot inline -s 900,450
%plot inline -r 120
figure();
subplot(211)
plot(tlsim(:,1),xlsim(:,1), 'b:', 'LineWidth', 1)
hold on
plot(t(1,1:end),x(1,1:end), 'r', 'LineWidth', 1)
grid on
plot(t(1,1:end),xnoisy(1,1:end), 'k:', 'LineWidth', 1.5)
legend (["lsim(ss)", "Ideal", "Noisy"])
xlabel("Time [s]"); ylabel("Position [m]"); title("Cart Response")

subplot(212)
plot(tlsim(:,1),xlsim(:,2), 'b:', 'LineWidth', 2)
hold on
plot(t(1,1:end),x(3,1:end), 'r', 'LineWidth', 1)
grid on
plot(t(1,1:end),xnoisy(3,1:end), 'k:', 'LineWidth', 1.5)
legend (["lsim(ss)", "Ideal", "Noisy"])
xlabel("Time [s]"); ylabel("Angle [$\theta$]",'Interpreter','latex'); title("Payload Response")

PART III: MULTIPLE OUTPUT CONTROLLER DESIGN FOR AN UNSTABLE NONLINEAR SYSTEM

Inverted Pendulum System

Let us apply a full state feedback controller to stabilize an inverted pendulum on a cart system.

The inverted pendulum model is a classic case in the study of control of mechanical systems. The system exhibits a combined rotation and translation and is nonlinear. The system is also a classic example of unstable systems. The Segway shown on Figure 3 Inverted Pendulum or what's commonly known as the "hoverboard" are examples of an inverted pendulum system.

The inverted pendulum is commonly modeled as a car moving laterally with a rod attached to it that rotates about a pivot fixed on the cart, with $\theta = 0$ when the rod is perfectly vertical. The input to the system is a force acting on the cart in the lateral direction, as shown on Figure 3

Figure 3 - Inverted Pendulum

The equations of motion for the above system are given as follows, note that they are derived from the crane model by substituting

$\theta_{\text{pendulum}} = \theta_{\text{crane}} + \pi$ ; giving $\sin\theta_{\text{pendulum}} = -sin\theta_{\text{cart}},$ and $\cos\theta_{\text{pendulum}} = -cos\theta_{\text{cart}}$ .

The equilibrium point is now defined where the rod is pointing upwards.

\begin{aligned} \left( m_{c} + m_{r} \right)\ddot{x} + b\dot{x} - m_{r}l\ddot{\theta}cos\theta +m_{r}l{\dot{\theta}}^{2}sin\theta = f(t)\\ \left( I + m_{r}l^{2} \right)\ddot{\theta} - m_{r}glsin\theta = m_{r}l\ddot{x}\text{cosθ} \end{aligned}

Where b is the coefficient of friction between the wheels and the surface, $m_{r}$ and $m_{c}$ are the rod and cart mass respectively, $I$ is the rod's moment of inertia about its center of mass, $l$ is the distance from the pivot to the center of mass for the rod and $g$ is the gravity constant.

After algebraic manipulation the decoupled (in the 2^nd^ derivative) model of the pendulum on a cart system is

\begin{aligned} \left( \left( I + m_{r}l^{2} \right)\left( m_{c} + m_{r} \right) - m_{r}^{2}l^{2}\cos^{2}\theta \right)\ddot{x} + \left( I + m_{r}l^{2} \right)m_{r}l{\dot{\theta}}^{2}cos\theta - m_{r}^{2}l^{2}gcos\theta sin\theta + \left( I + m_{r}l^{2} \right)b\dot{x} = \left( I + m_{r}l^{2} \right)f(t) \\ \left( \left( m_{r} + m_{c} \right)\left( I + m_{r}l^{2} \right) - m_{r}^{2}l^{2}\cos^{2}\theta \right)\ddot{\theta} - b\dot{x} - m_{r}\text{lcosθ}{\dot{\theta}}^{2} - \left( m_{r} + m_{c} \right)m_{r}glsin\theta = m_{r}lcos\theta f(t) \end{aligned}

Using the same model parameters as in Part II

III.A Linearizing, Modeling in State-Space Form

EXERCISE 9

Using the Crane model function file provided, create a new one to model the inverted pendulum by comparing the EOM in equations (2) with equations (9).

It is just a few sign changes from the Crane model
To animate the pendulum, flip the sign of rod line (lines 92 and 103-104)

Create another model with input disturbace $\omega$ that is zero mean with $\sigma = 50$ .

Linearize the inverted pendulum model above from the equations above and construct the state-space representation of the system. Provide your answer within the MATLAB script. Construct your output vector as $y = \begin{bmatrix} x \\ \theta \\ \end{bmatrix} = \begin{bmatrix} x_{1} \\ x_{3} \\ \end{bmatrix}$

To linearize: assume the following approximations: $sin\theta \approx \theta,cos\theta \approx 1,{\dot{\theta}}^{2} \approx 0$
Again, a few sign changes compared to the crane state-space model.

clear all;
mr = 2; mc = 10; I = 0.106; b = 20; l = .4; g = 9.81;
Den = ((I + mr*l^2) * (mc + mr) - mr^2 * l^2);
A = [
    0, 1, 0, 0;
    0, -(I + mr*l^2)*b/Den, +mr^2*l^2*g/Den, 0; 
    0, 0, 0, 1;
    0, b/Den, +(mr + mc)*mr*g*l, 0
    ];
B = [0; (I + mr*l^2)/Den; 0; mr*l/Den];
C = [1 0 0 0; 0 0 1 0];
D = [0; 0];

[num,den] = ss2tf(A,B,C,D);
Ginv_cart = tf(num(1,:),den)
Ginv_pendulum = tf(num(2,:),den)

Ginv_cart =
     
        0.09526 s^2 - 1.692e-16 s - 8.72
      -------------------------------------
      s^4 + 1.905 s^3 - 94.18 s^2 - 185.7 s
     
    Continuous-time transfer function.
    
    
    Ginv_pendulum =
     
              0.1789 s^2 + 0.7668 s
      -------------------------------------
      s^4 + 1.905 s^3 - 94.18 s^2 - 185.7 s
     
    Continuous-time transfer function.

III.B Inverted Pendulum Control via Full State Feedback – Pole Placement

EXERCISE 10

Simulate the response of the closed-loop system using lsim(), with $r = 0$ and initial condition $x_{0} = \begin{bmatrix} 0 & 0 & \pi\text{/}2 & 0 \\ \end{bmatrix}^{T}$ . Repeat tasks 1 & 2 until you achieve a stable response and settling time for both the cart and pendulum of $T_{s} < 10s$ (the pendulum reaches $\theta \approx 0rad$ and cart reaches $x \approx 0m$ as well, in under 10s)

Plot the position variables $x,\theta$ in one subplot, the velocity variables $\dot{x},\dot{\theta}$ in another subplot.

Implement your controller in the inverted pendulum simulation provided, with and without disturbance.

dt = 0.0001;
t = 0:dt:10;

p1 = -2.75 + 1.25;
p2 = -2.75 - 1.25;
p3 = -7.5;
p4 = -13;
K = place(A,B,[p1 p2 p3 p4]);
sys_cl = ss(A-B*K,B,C,0);

dxdt = @(t,x,u) [
    x(2);
    ((I + mr*l^2) * u - (I + mr*l^2)*mr*l*x(4)^2*cos(x(3)) + mr^2*l^2*g*cos(x(3))*sin(x(3))...
    - (I + mr*l^2)*b*x(2)) / ((I + mr*l^2)*(mc + mr) - mr^2*l^2*cos(x(3))^2);
    x(4);  
    (b*x(2) + mr*l*cos(x(3))*x(4)^2 + (mr + mc)*mr*g*l*sin(x(3)) + mr * l * cos(x(3))* u) /...
    ((I + mr*l^2)*(mc + mr) - mr^2*l^2*cos(x(3))^2) 
    ];
    
dxdt_noisy = @(t,x,u) [
    x(2);
    ((I + mr*l^2) * (u+100*randn()) - (I + mr*l^2)*mr*l*x(4)^2*cos(x(3)) + mr^2*l^2*g*cos(x(3))*sin(x(3))...
    - (I + mr*l^2)*b*x(2)) / ((I + mr*l^2)*(mc + mr) - mr^2*l^2*cos(x(3))^2);
    x(4);  
    (b*x(2) + mr*l*cos(x(3))*x(4)^2 + (mr + mc)*mr*g*l*sin(x(3)) + mr * l * cos(x(3))* (u+100*randn())) /...
    ((I + mr*l^2)*(mc + mr) - mr^2*l^2*cos(x(3))^2) 
    ];
    
r = t*0;
x0 = [0; 0; 1.5; 0];
[xlsim,tlsim] = lsim(sys_cl,r,t,x0);

% Initialize Simulation Vectors
x = zeros(4, length(t));
xnoisy = zeros(4, length(t));
u = zeros(1, length(t));
unoisy = zeros(1, length(t));
e = zeros(1, length(t));
enoisy = zeros(1, length(t));

% Initial Condition - Explicit Declaration
x(:,1) = x0;
xnoisy(:,1) = x0;

Kp = -0.7; Ki = 0; Kd = -70;

% Discrete controller gains
Ka = Kp + Ki * dt / 2 + Kd / dt;
Kb = -Kp + Ki * dt / 2 - 2 * Kd / dt;
Kc = Kd/dt;

% Step Input r = 0
r = 0;

% Simulate 
for idx = 1:length(t)

    u(1, idx) = r - K*x(:,idx);
    unoisy(1, idx) = r - K*xnoisy(:,idx);
    
    xdot = dxdt(t(1, idx), x(:,idx), u(1,idx));
    xdot_noisy = dxdt_noisy(t(1, idx), xnoisy(:,idx), unoisy(1,idx));
    
    % Integrate state
    if(idx < length(t))
        x(:,idx+1) = x(:,idx) + xdot*dt;
        xnoisy(:,idx+1) = xnoisy(:,idx) + xdot_noisy*dt;
    end
end

%% BLOTTING
%plot inline --format=svg
%plot inline -s 900,450
%plot inline -r 120
figure();
subplot(211)
plot(tlsim(:,1),xlsim(:,1), 'b:', 'LineWidth', 1)
hold on
plot(t(1,1:end),x(1,1:end), 'r', 'LineWidth', 1)
grid on
plot(t(1,1:end),xnoisy(1,1:end), 'k:', 'LineWidth', 1.5)
legend (["lsim(ss)", "Ideal", "Noisy"])
xlabel("Time [s]"); ylabel("Position [m]"); title("Cart Response")

subplot(212)
plot(tlsim(:,1),xlsim(:,2), 'b:', 'LineWidth', 2)
hold on
plot(t(1,1:end),x(3,1:end), 'r', 'LineWidth', 1)
grid on
plot(t(1,1:end),xnoisy(3,1:end), 'k:', 'LineWidth', 1.5)
legend (["lsim(ss)", "Ideal", "Noisy"])
xlabel("Time [s]"); ylabel("Angle [$\theta$]",'Interpreter','latex'); title("Payload Response")

tplace = t; xplace = xnoisy;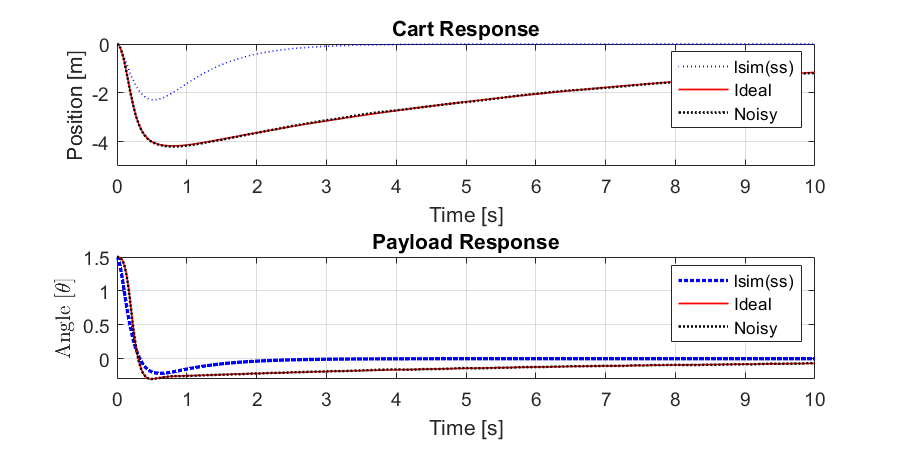

III.C Inverted Pendulum Control via Full State Feedback – Linear Quadratic Regulator (LQR)

EXERCISE 11

Use the Linear Quadratic Regulator to compute the gain matrix K and simulate the response with disturbance, try to achieve a settling time for both the cart and pendulum of $T_{s} < 5s$ . Compare the poles computed by the LQR method with the poles you've guessed earlier.

Look up the $lqr()$ function and MATLAB.

%% LQR Design
Q = eye(4);
Q(1,1) = 100^2;
Q(2,2) = 10^2;
Q(3,3) = 60^2;
Q(4,4) = 10^2;
R = 1;
N = 0;
[K, S, P] = lqr(A,B,Q,R,N); 

sys_cl = ss(A-B*K,B,C,0);

dxdt = @(t,x,u) [
    x(2);
    ((I + mr*l^2) * u - (I + mr*l^2)*mr*l*x(4)^2*cos(x(3)) + mr^2*l^2*g*cos(x(3))*sin(x(3))...
    - (I + mr*l^2)*b*x(2)) / ((I + mr*l^2)*(mc + mr) - mr^2*l^2*cos(x(3))^2);
    x(4);  
    (b*x(2) + mr*l*cos(x(3))*x(4)^2 + (mr + mc)*mr*g*l*sin(x(3)) + mr * l * cos(x(3))* u) /...
    ((I + mr*l^2)*(mc + mr) - mr^2*l^2*cos(x(3))^2) 
    ];
    
dxdt_noisy = @(t,x,u) [
    x(2);
    ((I + mr*l^2) * (u+100*randn()) - (I + mr*l^2)*mr*l*x(4)^2*cos(x(3)) + mr^2*l^2*g*cos(x(3))*sin(x(3))...
    - (I + mr*l^2)*b*x(2)) / ((I + mr*l^2)*(mc + mr) - mr^2*l^2*cos(x(3))^2);
    x(4);  
    (b*x(2) + mr*l*cos(x(3))*x(4)^2 + (mr + mc)*mr*g*l*sin(x(3)) + mr * l * cos(x(3))* (u+100*randn())) /...
    ((I + mr*l^2)*(mc + mr) - mr^2*l^2*cos(x(3))^2) 
    ];
    
r = t*0;
x0 = [0; 0; 1.5; 0];
[xlsim,tlsim] = lsim(sys_cl,r,t,x0);

% Initialize Simulation Vectors
x = zeros(4, length(t));
xnoisy = zeros(4, length(t));
u = zeros(1, length(t));
unoisy = zeros(1, length(t));
e = zeros(1, length(t));
enoisy = zeros(1, length(t));

% Initial Condition - Explicit Declaration
x(:,1) = x0;
xnoisy(:,1) = x0;

Kp = -0.7; Ki = 0; Kd = -70;

% Discrete controller gains
Ka = Kp + Ki * dt / 2 + Kd / dt;
Kb = -Kp + Ki * dt / 2 - 2 * Kd / dt;
Kc = Kd/dt;

% Step Input r = 0
r = 0;

% Simulate 
for idx = 1:length(t)

    u(1, idx) = r - K*x(:,idx);
    unoisy(1, idx) = r - K*xnoisy(:,idx);
    
    xdot = dxdt(t(1, idx), x(:,idx), u(1,idx));
    xdot_noisy = dxdt_noisy(t(1, idx), xnoisy(:,idx), unoisy(1,idx));
    
    % Integrate state
    if(idx < length(t))
        x(:,idx+1) = x(:,idx) + xdot*dt;
        xnoisy(:,idx+1) = xnoisy(:,idx) + xdot_noisy*dt;
    end
end

%% BLOTTING
%plot inline --format=svg
%plot inline -s 900,450
%plot inline -r 120
figure();
subplot(211)
plot(tlsim(:,1),xlsim(:,1), 'b:', 'LineWidth', 1)
hold on
plot(t(1,1:end),x(1,1:end), 'r', 'LineWidth', 1)
grid on
plot(t(1,1:end),xnoisy(1,1:end), 'k:', 'LineWidth', 1.5)
legend (["lsim(ss)", "Ideal", "Noisy"])
xlabel("Time [s]"); ylabel("Position [m]"); title("Cart Response")

subplot(212)
plot(tlsim(:,1),xlsim(:,2), 'b:', 'LineWidth', 2)
hold on
plot(t(1,1:end),x(3,1:end), 'r', 'LineWidth', 1)
grid on
plot(t(1,1:end),xnoisy(3,1:end), 'k:', 'LineWidth', 1.5)
legend (["lsim(ss)", "Ideal", "Noisy"])
xlabel("Time [s]"); ylabel("Angle [$\theta$]",'Interpreter','latex'); title("Payload Response")

tlqr = t; xlqr = xnoisy;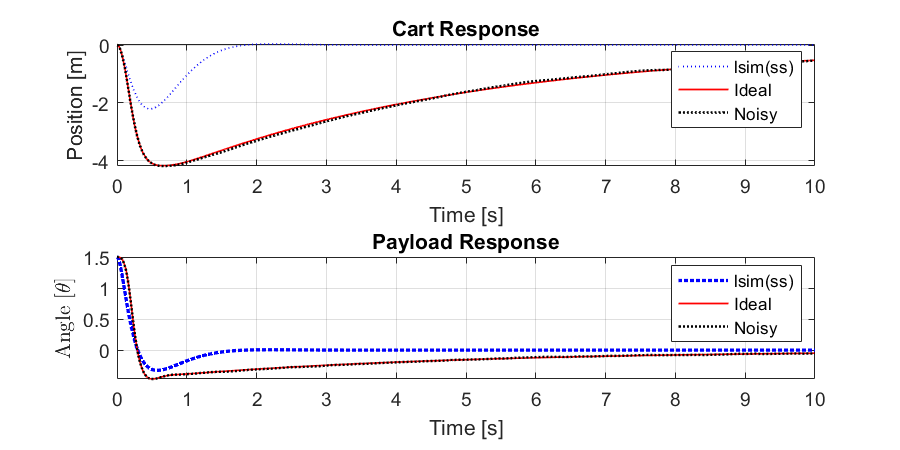

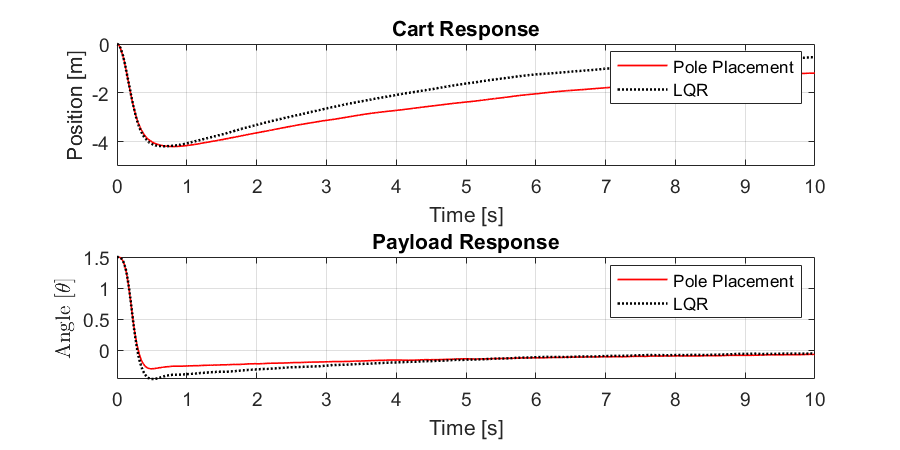
Now let's compare between the Pole Placement method and LQR method

%% BLOTTING
%plot inline --format=svg
%plot inline -s 900,450
%plot inline -r 120
figure();
subplot(211)
plot(tplace(1,1:end),xplace(1,1:end), 'r', 'LineWidth', 1)
hold on
grid on
plot(tlqr(1,1:end),xlqr(1,1:end), 'k:', 'LineWidth', 1.5)
legend (["Pole Placement", "LQR"])
xlabel("Time [s]"); ylabel("Position [m]"); title("Cart Response")

subplot(212)
plot(tplace(1,1:end),xplace(3,1:end), 'r', 'LineWidth', 1)
hold on
grid on
plot(tlqr(1,1:end),xlqr(3,1:end), 'k:', 'LineWidth', 1.5)
legend (["Pole Placement", "LQR"])
xlabel("Time [s]"); ylabel("Angle [$\theta$]",'Interpreter','latex'); title("Payload Response")