Implementing a PID Controller in Numerical Integration Simulation

This note explains how to simulate the closed-loop response of a system that has a zero with a PID controller, using basic numerical integration.

Consider the following system, $G_p=\dfrac{3(s+3)}{s^2+3s+15}$, for which we want to apply the controller $G_c=0.007(s+20)\dfrac{s+6}{s}$ in unity feedback.

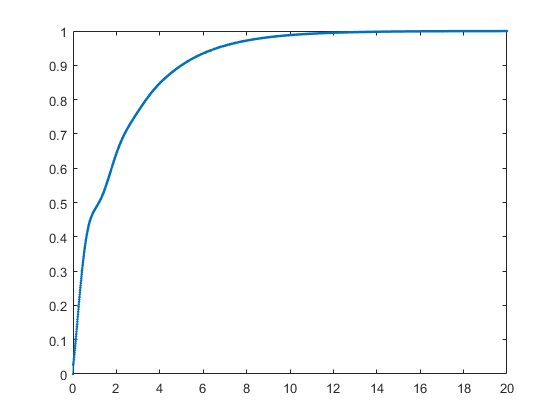
If we want to simulate the closed-loop response to a step input, using the built-in functions, we can compute the direct closed-loop transfer function. $G_{cl}=\dfrac{G_cG_p}{1+G_cG_p}$

Then we can directly use the step() response function.

s = tf("s")
Gp = 3*(s+3) / (s^2+3*s+15)
Gc = 0.007*(s+20)*(s+6)/s
Gcl = feedback(Gc*Gp, 1)
figure()
step(Gcl)

s =
  
      s
     
    Continuous-time transfer function.
    
    
    Gp =
     
         3 s + 9
      --------------
      s^2 + 3 s + 15
     
    Continuous-time transfer function.
    
    
    Gc =
     
      0.007 s^2 + 0.182 s + 0.84
      --------------------------
                  s
     
    Continuous-time transfer function.
    
    
    Gcl =
     
      0.021 s^3 + 0.609 s^2 + 4.158 s + 7.56
      --------------------------------------
      1.021 s^3 + 3.609 s^2 + 19.16 s + 7.56
     
    Continuous-time transfer function.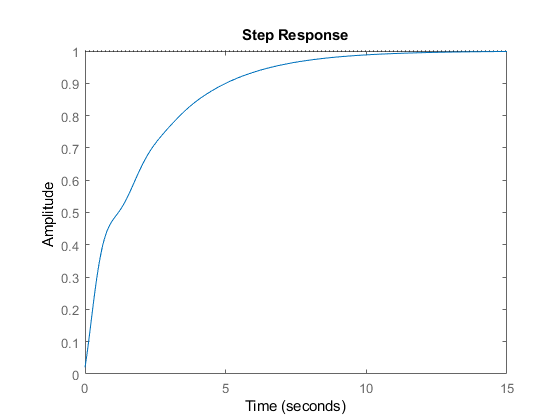

PID Controller - Continuous Form

But we want to simulate the response through basic numerical integration. Let's look at the PID control law

And in code form

u[idx] = Kp*e[idx] + Ki*eint[idx] + Kd*edot[idx]

We can find the integral and derivative of the error by numerical integration and differentiation respectively, this is really a discrete controller, it will not produce the same response as we got with step(), but will be close if $\Delta t$ is sufficiently small.

To find the error, error integral and error derivative numerically, where r is the reference and y is the output of the system, and dt is the time sample of the simulation. We can do the following

e[idx] = r[idx] - y[idx]
eint[idx] = eint[idx-1]+ e[idx] * dt;
edot[idx] = (e[idx] - e[idx -1]) / dt;

Note that on the first iteration, we can not access a negative index, so you can keep eint[1]=e[1]*dt and edot[1]=0, then apply the above rules for idx>1

Simulating a system response with a zero

Converting the transfer function $G(s)=\dfrac{Y}{U}=\dfrac{2(s+30)}{s^2+4s+20}$ to a differential equation, we get $\ddot{y}+3\dot{y}+15y=3\dot{u}+9u$. This is a second order system, and to express it as a state-space vector model, we require two states.

But note that to implement it numerically, we would have to differentiate the input signal. A better approach is to separate the zeros of the plant transfer function, and rather than differentiate the input, scale the state by the numerator to produce the output (no differentiation necessary). Note that the plant can be separated as $G_p=\dfrac{Y}{U}=\dfrac{Y}{X}\dfrac{X}{U}=(3s+9)\dfrac{1}{s^2+3s+9}$, we can convert each of $\dfrac{X}{U}$ and $\dfrac{Y}{X}$ into a differential equation and we get: $\ddot{x}+3\dot{x}+15x=u$, and $y=3\dot{x}+9x$. Expressed numerically.

dxdt=@(t,x,u) [x(2); (-3*x(2)-15*x(1)+u)];

Where

y[idx] = 3*xdot[idx]+9*x[idx];

e[idx] = r[idx] - y[idx]
eint[idx] = eint[idx-1]+ e[idx] * dt;
edot[idx] = (e[idx] - e[idx -1]) / dt;

u[idx] = Kp*e[idx] + Ki*eint[idx] + Kd*edot[idx]

And there is no need to differentiate the input signal now.

Let's see how all this can be simulated. Note that the PID controller gains are $K_P=.182, K_D=0.007, K_I=0.84$

dxdt=@(t,x,u) [x(2); (-3*x(2)-15*x(1)+u)];

% Integration time-step
dt = 0.01;

% Time vector
t = 0:dt:20;

% Initialize Simulation Vectors
x = zeros(2, length(t));
y = zeros(1, length(t));
u = zeros(1, length(t));
e = zeros(1, length(t));
edot = e; 
eint = e;

% Initial Condition - Explicit Declaration
x0 = [0; 0];
x(:,1) = x0;

% Controller Gains
Kp=.182; Kd = 0.007; Ki=0.84;

% Step Input r = 1
r = 1;

% Simulate 
for idx = 1:length(t)
    e(1, idx)   = r - y(1,idx);
    if idx == 1
        eint(1,idx) = e(1,idx) * dt; % Forward Integration
        edot(1,idx) = 0; % Skip on first iteration        
    else
        eint(1,idx) = eint(1,idx-1) + e(1,idx) * dt;
        edot(1,idx) = (e(1,idx) - e(1, idx-1)) / dt;
    end
    u(1,idx) = Kp*e(1,idx) + Ki*eint(1,idx) + Kd*edot(1,idx);
    xdot = dxdt(t(1, idx), x(:,idx), u(1,idx));

    % Integrate state
    if(idx < length(t))
        x(:,idx+1) = x(:,idx) + xdot.*dt;
        % Scale output
        y(1, idx+1) = 9*x(1,idx+1)+3*x(2,idx+1);
    end
     
end

figure()
step(Gcl)
hold on
plot(t(1,1:end),y(1,1:end), ':')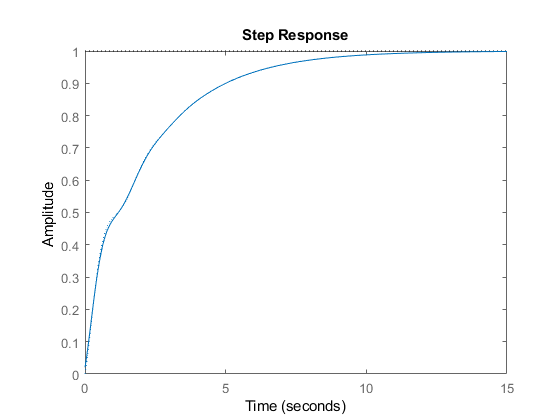

PID Controller - Discrete Form

A numerical integration simulation is a discrete system simulation, and converges into a continuous system for small $\Delta t$, in addition, differentiating signal boundaries results in errors, and basic numerical integration is insufficient.

Given a continous form PID controller $G_c=\dfrac{K_Ds^2+K_Ps+K_I}{s}$, we can convert it into a discrete form then derive the difference equation. This is outside the scope of this class, but here is the difference equation form of a PID controller.

u[k]=u[k-1] + a*e[idx] + b*e[idx-1] + c*e[idx-1]

where

Note that the discrete PID gains are a function of the continous PID gains in addition to the sampling (integration) time-step.

Let's substitute this in the simulation setup and see if it works.

dxdt=@(t,x,u) [x(2); (-3*x(2)-15*x(1)+u)];

% Integration time-step
dt = 0.01;

% Time vector
t = 0:dt:20;

% Initialize Simulation Vectors
x = zeros(2, length(t));
y = zeros(1, length(t));
u = zeros(1, length(t));
e = zeros(1, length(t));

% Initial Condition - Explicit Declaration
x0 = [0; 0];
x(:,1) = x0;

% Controller Gains
Kp=.182; Kd = 0.007; Ki=0.84;
% Discrete controller gains
a = Kp + Ki * dt / 2 + Kd / dt;
b = -Kp + Ki * dt / 2 - 2 * Kd / dt;
c = Kd/dt;

% Step Input r = 1
r = 1;

% Simulate 
for idx = 1:length(t)
    e(1, idx)   = r - y(1,idx);
    if idx > 2
        u(1,idx) = u(1,idx-1) + a*e(1,idx) +b*e(1,idx-1) + c*e(1,idx-2);
    elseif idx == 2
        u(1,idx) = u(1,idx-1) + a*e(1,idx) +b*e(1,idx-1);
    elseif idx == 1
        u(1,idx) = a*e(1,idx); 
    end
    xdot = dxdt(t(1, idx), x(:,idx), u(1,idx));
    % Integrate state
    if(idx < length(t))
        x(:,idx+1) = x(:,idx) + xdot*dt;
        % Scale output
        y(1, idx+1) = 9*x(1,idx+1)+3*x(2,idx+1);
    end
end
plot(t(1,1:end),y(1,1:end), '.-')